Instabilità numerica, divergenza e previsione dell'iterazione
Oltre alla verifica di convergenza, alla fine di ciascun passo di iterazione sono possibili altre tre verifiche della soluzione: (i) instabilità numerica, (ii) divergenza della soluzione e (iii) previsione dell'iterazione. Questi criteri, tutti del tipo 'forza/momento', servono per evitare inutili iterazioni nel caso in cui è evidente che non potrà essere raggiunta la convergenza, minimizzando così la durata dell'analisi.
Instabilità numerica
La possibilità che una soluzione diventi numericamente instabile è controllata ad ogni iterazione confrontando la norma euclidea dei carichi non bilanciati, Gnorm, con una tolleranza massima predefinita (valore di default=1.0E+20), di diversi ordini di grandezza maggiore del vettore dei carichi applicato. Se Gnorm supera questa tolleranza, allora la soluzione è assunta essere numericamente instabile e le iterazioni nell'incremento corrente sono interrotte, con un 'log flag message' uguale a Max_Tol.
In alcune occasioni può capitare che modelli molto instabili possano condurre ad un improvviso sviluppo di forze non bilanciate (out-of-balance forces) che sono diversi ordini di grandezza più grandi del valore massimo di tolleranza. Questo, a sua volta, crea un cosiddetto Problema di soluzione (cioè, l'analisi si interrompe anche se in modo "pulito") e le iterazioni all'interno dell'incremento corrente sono interrotte, con un 'log flag message' uguale a Sol_Prb.
Divergenza della soluzione
La divergenza della soluzione è controllata confrontando il valore di Gnorm ottenuto nell'iterazione corrente con quello ottenuto nell'iterazione precedente. Se Gnorm è aumentato, allora si assume che la soluzione sta divergendo e le iterazioni nell'incremento corrente sono interrotte, con un 'log flag message' uguale a Diverge.
Previsione dell'iterazione
Infine viene fatta anche una verifica sull'incremento logaritmico di convergenza al fine di prevedere il numero di iterazioni (itepred) richieste per raggiungere la convergenza. Se itepred è maggiore del numero massimo di iterazioni specificato dall'utente, allora si assume che la soluzione non raggiungerà la convergenza e le iterazioni nell'incremento corrente sono interrotte, con un 'log flag message' uguale a Prd_Ite.
Per calcolare il valore di itepred è impiegata la seguente equazione, in cui ite rappresenta il numero corrente di iterazioni e Gtol è la tolleranza forza/momento:
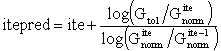
Nell'ambito delle analisi svolte con SeismoStruct le tre verifiche descritte sopra sono solitamente affidabili ed efficaci, purchè le verifiche di divergenza e di previsione dell'iterazione non vengano effettuate durante le prime iterazioni di ciascun passo incrementale, quando la soluzione potrebbe non essere ancora sufficientemente stabile. Questo argomento è discusso in maggior dettaglio nella sezione sulla Strategia Iterativa, dove sono descritti tutti i parametri in relazione con questi criteri.
Nota: Alcuni tipi di elementi (infrmFB, infrmFBPH, infrmDBPH e masonry) richiedono un certo numero di iterazioni da svolgere per poter raggiungere l'equilibrio interno. In alcuni casi l'equilibrio ciclico per l'elemento non può essere raggiunto, come segnalato dai 'log flag messages' elm_inv e elm_ite. Si prega di far riferimento qui per ulteriori informazioni su questo tema.