Inelasticità del materiale

Gli elementi a plasticità diffusa vengono sempre più impiegati nelle applicazioni dell'ingegneria sismica, sia per scopi di ricerca che nell'ambito tecnico-professionale. Se i vantaggi di questi elementi, rispetto ai più semplici modelli a plasticità concentrata, sono largamente elencati, ad esempio, nelle pubblicazioni di Filippou and Fenves [2004] o di Fragiadakis and Papadrakakis [2008], insieme ad una breve descrizione della loro evoluzione storica ed alla discussione sulle limitazioni esistenti, in questa sede si vuol far semplicemente notare come gli elementi a plasticità diffusa non richiedano una calibrazione dei parametri di risposta empirici (non necessariamente diretta) per ottenere la risposta di un elemento reale o ideale sotto condizioni di carico idealizzate, come invece è necessario fare nel caso dei modelli a plasticità concentrata.

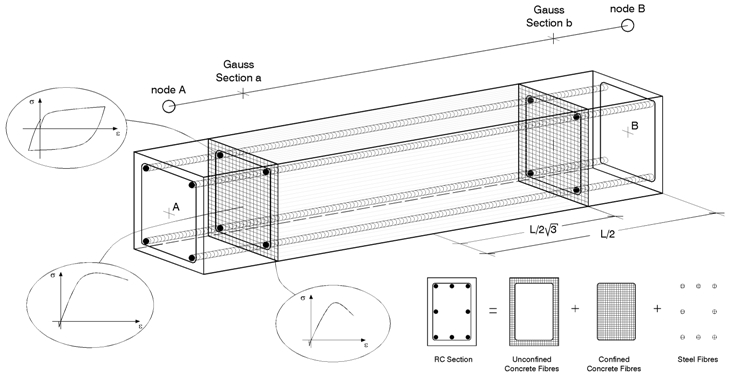
In SeismoStruct si fa uso del cosiddetto 'approccio a fibre' per rappresentare il comportamento di una sezione. In questo approccio ad ogni fibra è associata una relazione uniassiale sforzo-deformazione (si veda la figura sottostante); lo stato tenso-deformativo delle sezioni degli elementi trave-colonna è pertanto ottenuto tramite l'integrazione della risposta uniassiale nonlineare sforzo-deformazione di ciascuna fibra (tipicamente 100-150) in cui è stata suddivisa la sezione (la discretizzazione di una tipica sezione in cemento armato è rappresentata, a titolo di esempio, nella figura sottostante).

Questo tipo di modellazione presenta, inoltre, numerosi vantaggi che possono essere riassunti nel seguito: (i) nessun obbligo di svolgere, per gli elementi, un'analisi propedeutica momento-curvatura, (ii) nessun bisogno di introdurre alcun tipo di comportamento isteretico associato agli elementi (dal momento che tale comportamento è implicitamente definito dai legami costitutivi dei materiali associati alla sezione), (iii) modellazione diretta dell'interazione carico assiale-momento (sia in termini di resistenza che di rigidezza), (iv) rappresentazione diretta del carico biassiale, e infine (v) interazione tra le resistenze flessionali nelle direzioni ortogonali.

Gli elementi a plasticità diffusa possono essere implementati con due diverse formulazioni agli elementi finiti: la classica formulazione basata sugli spostamenti (displacement-based) (nel seguito denominata DB) [ad es. Hellesland and Scordelis 1981; Mari and Scordelis 1984], e la più recente formulazione basata sulle forze (force-based) (nel seguito denominata FB) [ad es. Spacone et al. 1996; Neuenhofer and Filippou 1997]. Nell'approccio basato sugli spostamenti (DB) viene imposto il campo degli spostamenti, mentre quando si impiega un elemento la cui formulazione è basata sulle forze (FB) l'equilibrio è strettamente soddisfatto e non sono posti vincoli allo sviluppo di deformazioni inelastiche in tutto l'elemento; si prega di far riferimento, ad esempio, alle seguenti pubblicazioni per ulteriori chiarimenti: Alemdar and White [2005] e Freitas et al. [1999].

Nell'approccio DB vengono impiegate funzioni di forma in spostamento che corrispondono, ad esempio, ad una variazione lineare della curvatura lungo l'elemento. Al contrario, nell'approccio FB viene imposta una variazione lineare del momento, cioè il duale della variazione lineare di curvatura precedentemente menzionata. Quando il comportamento del materiale è elastico-lineare, i due approcci ovviamente producono gli stessi risultati (questo è dovuto al fatto che solo le forze nodali agiscono sull'elemento). Al contrario, quando il comportamento del materiale è inelastico, con l'imposizione di un campo di spostamenti non si riesce a catturare la vera deformata poiché il campo di curvatura può essere, in un caso generale, altamente nonlineare. In questa situazione, se si utilizza la formulazione basata sugli spostamenti è necessario procedere con una discretizzazione (meshing) raffinata dell'elemento strutturale (tipicamente 4-5 elementi per ciascun elemento strutturale) per il calcolo di forze/spostamenti nodali, al fine di accettare l'ipotesi di un campo di curvatura lineare all'interno di ciascun sottodominio. Tuttavia, in quest'ultimo caso gli utenti sono invitati a non fare affidamento sui valori delle curvature di sezione calcolate e sugli stati di sforzo-deformazione delle singole fibre.

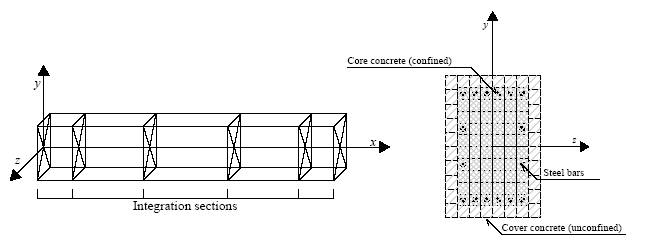
Viceversa, la formulazione basata sulle forze è sempre esatta, in quanto non dipende dal comportamento costitutivo assunto per la sezione. Infatti, non limita in alcun modo il campo degli spostamenti dell'elemento. Pertanto, in questo senso questa seconda formulazione può essere considerata come 'esatta', con l'unica approssimazione introdotta dalla definizione di un discreto numero di sezioni di controllo lungo l'elemento, le quali vengono usate per l'integrazione numerica. È richiesto un numero minimo di 3 sezioni d'integrazione Gauss-Lobatto per evitare sotto-integrazione, tuttavia tale opzione non sarà, in generale, in grado di simulare la diffusione dell'inelasticità in modo accettabile. Di conseguenza, il numero minimo di punti di integrazione proposto è 4, anche se in genere vengono utilizzati 5-7 IP (vedi figura sotto) Tale caratteristica consente di modellare ciascun elemento strutturale con un solo elemento finito, permettendo così una corrispondenza biunivoca (one-to-one) tra l'elemento strutturale (trave o pilastro) e l'elemento finito. In altre parole, adottando la formulazione FB teoricamente non è necessario discretizzare gli elementi, a meno che non ci siano variazioni della sezione lungo l'elemento; questo perché il campo delle forze è sempre esatto, indipendentemente dal livello di nonlinearità.

In SeismoStruct sono implementate entrambe le formulazioni citate sopra (DB e FB). La formulazione basata sulle forze, però, è generalmente consigliata poiché, come già detto, nella maggior parte dei casi non richiede la suddivisione degli elementi. Questa scelta porta ad avere modelli decisamente più contenuti (in termini di numero di elementi) e gestibili rispetto a quelli ottenuti impiegando elementi con formulazione basata sugli spostamenti; ciò comporta analisi molto più veloci, nonostante i calcoli per il raggiungimento dell'equilibrio dell'elemento siano più pesanti. Un'eccezione a questa regola di 'non-discretizzazione', però, deve essere fatta quando sono attesi effetti di localizzazione; nel qual caso sono necessarie particolari cautele/precauzioni, come discusso in Calabrese et al. [2010].

Inoltre, l'uso di un singolo elemento finito per elemento strutturale offre all'utente la possibilità di utilizzare facilmente i risultati delle rotazioni alla corda degli elementi per le verifiche sismiche secondo le normative vigenti (ad es. Norme Tecniche per le Costruzioni 2008, Eurocodice 8, ASCE/SEI 7-05, ecc.). Invece, nel caso in cui l'elemento strutturale sia stato discretizzato in due o più elementi (quello che necessariamente avviene nel caso si utilizzino elementi con formulazione basata sugli spostamenti), è necessario post-processare gli spostamenti/rotazioni nodali al fine di valutare le rotazioni alla corda degli elementi stessi [ad es. Mpampatsikos et al. 2008].

Infine, si sottolinea che in SeismoStruct è impiegata la quadratura di Gauss-Legendre per gli elementi DB (che fanno uso di due sezioni d'integrazione), mentre la quadratura di Gauss-Lobatto viene utilizzata per gli elementi FB (che sono caratterizzati da 4 a 10 sezioni d'integrazione). Sebbene gli utenti possano e debbano far riferimento alla letteratura (o a questa fonte online) per ulteriori dettagli sulle regole in questione, le coordinate approssimative lungo la lunghezza dell'elemento (misurate dal suo baricentro) delle sezioni d'integrazione sono le seguenti:

• 2 sezioni d'integrazione: [-0.577  0.577] x L/2
• 3 sezioni d'integrazione: [-1  0.0  1] x L/2
• 4 sezioni d'integrazione: [-1  -0.447  0.447  1] x L/2
• 5 sezioni d'integrazione: [-1  -0.655  0.0  0.655  1] x L/2
• 6 sezioni d'integrazione: [-1  -0.765  -0.285  0.285  0.765  1] x L/2
• 7 sezioni d'integrazione: [-1  -0.830  -0.469  0.0  0.469  0.830  1] x L/2
• 8 sezioni d'integrazione: [-1  -0.872  -0.592  -0.209  0.209  0.592  0.872  1] x L/2
• 9 sezioni d'integrazione: [-1  -0.900  -0.677  -0.363  0.0  0.363  0.677  0.900  1] x L/2
• 10 sezioni d'integrazione: [-1  -0.920  -0.739  -0.478  -0.165  0.165  0.478  0.739  0.920  1] x L/2

Note

1. Con la formulazione basata sulle forze è immediato prendere in considerazione le sollecitazioni derivanti dai carichi agenti lungo gli elementi; seguendo invece l'approccio basato sugli spostamenti, i carichi distribuiti devono essere trasformati in carichi puntuali equivalenti (forze/momenti) posti ai nodi d'estremità (e poi deve essere svolta una lunga operazione di stress-recovery per recuperare le corrette sollecitazioni sugli elementi).
2. Qualora l'utente lo desiderasse, è possibile adottare un approccio a plasticità concentrata impiegando l’elemento frame inelastico con formulazione basata sugli spostamenti e cerniera plastica (infrmDBPH), come alternativa alla filosofia di modellazione a plasticità diffusa che è intrinseca negli altri elementi trave-colonna di SeismoStruct – per esempio, l’elemento inelastico con formulazione basata sulle forze e cerniera plastica (infrmFBPH) concentra anch’esso l’inelasticità ai due estremi, tuttavia all'interno di una lunghezza dell'elemento prefissata. Lo stesso effetto di modellazione può essere raggiunto utilizzando elementi trave-colonna elastici (elfrm) accoppiati a elementi link nonlineari posti nei nodi d'estremità dell'elemento strutturale. Questo tipo di modellazione dovrebbe comunque essere utilizzato con cautela, in quanto l'accuratezza dell'analisi potrebbe essere compromessa qualora l'utente non avesse sufficiente esperienza nella calibrazione delle curve di risposta impiegate per la definizione degli elementi 'link': la natura disaccoppiata dei diversi gradi di libertà non permette inoltre di modellare le curve/superfici di interazione azione assiale/momento.
3. Come discusso sopra, la modellazione a plasticità diffusa non richiede alcuna esperienza di modellazione avanzata, in quanto tutto ciò che è richiesto all'utente è l'introduzione delle caratteristiche geometriche e del materiale per gli elementi strutturali (ossia i parametri ingegneristici). Il suo utilizzo è quindi vivamente consigliato, in quanto garanzia di un'accurata previsione della risposta nonlineare della struttura.
4. Gli utenti sono anche invitati a leggere il NEHRP Seismic Design Technical Brief No. 4, in cui viene bene trattata la modellazione nonlineare.