Macro-elemento Interazione Suolo-Struttura per Fondazioni Profonde (su pali) SSI2 - ssilink2
Questo elemento estende l’approccio a macro-elemento non lineare all’analisi di pali flessibili caricati lateralmente e interazione suolo-struttura. È basata sul lavoro di Correia e Pecker [2019b].La risposta laterale dell’intero sistema palo-terreno all’azione sismica viene concentrata tutta alla testa del palo, essendo rappresentata da un elemento zero-lenght collocato alla base dei pilastri e soggetto all’input motorio delle fondazioni, come mostrato nella figura sottostante.
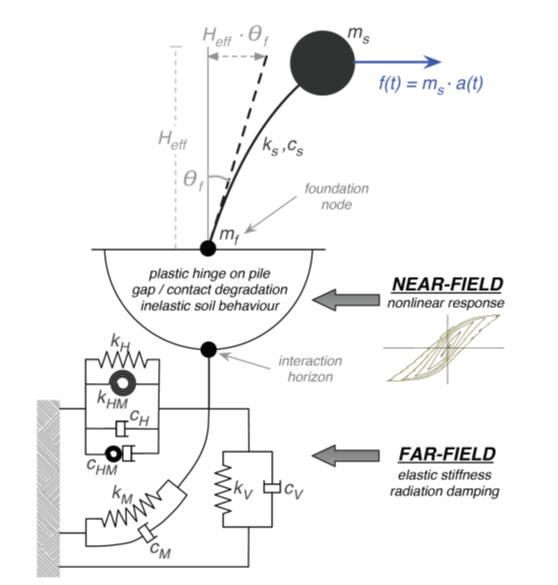
Il macro-elemento palo rappresenta il comportamento laterale di un singolo palo, soggetto a carichi e momenti orizzontali, dalla fase iniziale di carico fino al raggiungimento del collasso. Gli effetti del carico verticale non sono direttamente considerati in questo modello ad eccezione dell’influenza del momento plastico della sezione trasversale. Altrimenti si considera che solo la zona superiore del profilo del terreno contribuisca solo alla resistenza ai carichi laterali, fino alla profondità alla quale si forma la cerniera plastica. Il carico verticale si assume sia trasferito al terreno circostante al di sotto della suddetta profondità, dove non vi è influenza del gap-opening.
Si considera un deposito di terreno saturo e al momento del sisma, si assume che sia impermeabile. Il suolo, è così considerato come se avesse un compotamento non drenato poiché lo scopo del macro-elemento è simulare la risposta del palo in condizioni sismiche, o cicli di carico a breve termine, è si assume che il criterio di rottura di Tresca sia valido. Nella figura sottostante si rappresentano due scenari geotecnici semplificati: (a) la distribuzione della resistenza a taglio non drenata (Su) lungo la profondità del deposito di terreno: costante o lineare; (b) la risposta per un palo caricato lateralmente, denominata: rottura del cuneo passivo di terreno a profondità ridotte e una rottura “flow-around” a maggiori profondità, con la possibilità della formazione di gap (palo-terreno) alle spalle del palo.

Il macro-elemento proposto è basato sulle tre principali caratteristiche del comportamento di pali caricati lateralmente, denominate:
-
risposta iniziale elastica;
-
apertura e chiusura del gap;
-
rottura per condizioni di carico.
Il modello plastico della bounding surface è utilizzato per rappresentare la continua transizione tra la risposta elastica iniziale e il flusso plastico a rottura, per condizioni di carico sul palo monotoniche e cicliche. Il comportamento di “gapping” è rappresentato da un modello non lineare elastico, che comunque, tiene in considerazione ed è influenzato dallo stato di deformazione plastica nel terreno circostante.
La bounding surface nel modello del macro-elemento corrisponde alla superficie di rottura per pali caricati lateralmente. Fin quando non vi sono evidenze di ciò, si può considerare il comportamento non associativo, la plasticità associativa è impiegata e la bounding surface agisce simultaneamente come superficie di potenziale plastico. Nella formulazione di questo macro-elemento non sono considerati gli effetti dei carichi assiali e, di conseguenza, la superficie di rottura è definita solamente in termini di forza orizzontale e momento del palo. Inoltre, si assume un carico di superficie.
È stata proposta da Correia e Pecker [2019a], una superficie di rottura pressoché “rotonda”, che si basa sulla “superellisse”. Si supponga che la superellisse abbia centro in (Hc, Mc), con asse orizzontale e asse verticale My, si impone inoltre una distorsione della sua forma, < 0, questa superficie di rottura approssimata può essere espressa come:
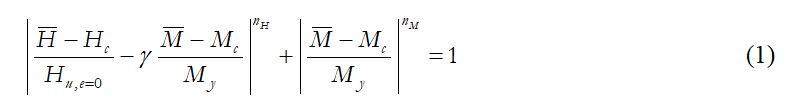
Gli esponenti positivo nH e nM controllano la curvatura ai lati della superellisse. La figura sottostante mostra la configurazione distorta della superellisse, centrata nell’origine (Hc = Mc = 0), con i parametri calibrati per rappresentare la superificie di rottura per profilo Su lineare.
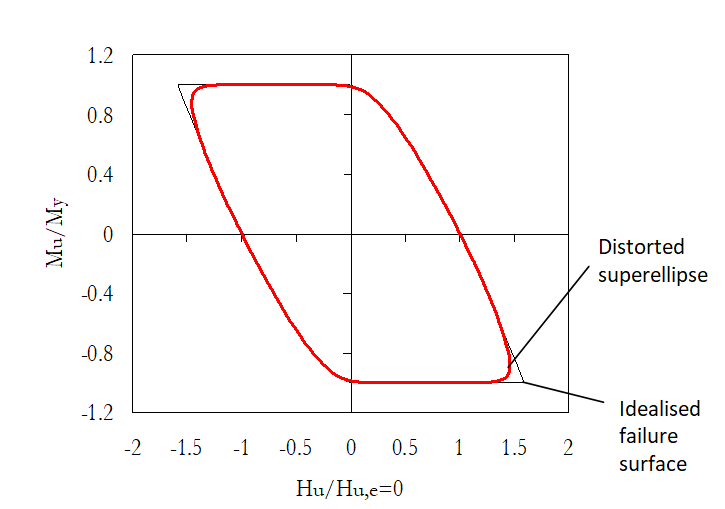
Il modello di macro-elemento richiede la definizione di 23 parametri:
-
il diametro del palo (DIAM)
-
la rigidezza del palo per le direzioni verticale, orizzontale e rotazionale (K_VV, K_HH, K_MM, K_HM, K_TT)
-
la capacità del palo (QQ_H_MAX, QQ_M_MAX)
-
i parametri della superellisse BS (Exp_nH,Exp_nM, GAMMA)
-
la massima profondità del gap (ZW)
-
la rigidezza flessionale del palo (Eplp)
-
il parametro di evoluzione del gap (BETA)
-
il parametro di evoluzione del gap minimo (ETA)
-
il parametro del modulo plastico di riferimento (PL_H0)
-
l'esponente di evoluzione del modulo plastico (PL_nur)
-
il limite inferiore per il delta in scarico/ricarico (DELTA_LIM)
La rigidezza flessionale del palo , può essere calcolata, mentee il momento di snervamento My, può essere calcolato utilizzando qualunque strumento di analisi della sezione trasversale ( e considerando il carico verticale sul palo). Espressioni per Hu, e=0 e zw, sono derivate da Correia e Pecker [2019a].
In Gazetas [1991] sono fornite le espressioni per il calcolo diretto della rigidezza laterale e assiale oltre al coefficiente di smorzamento. Queste sono valide per per profili di suolo con incremento di rigidezza del terreno lungo la profondità costante, lineare o parabolico, che sono rappresentati nella figura sottostante.
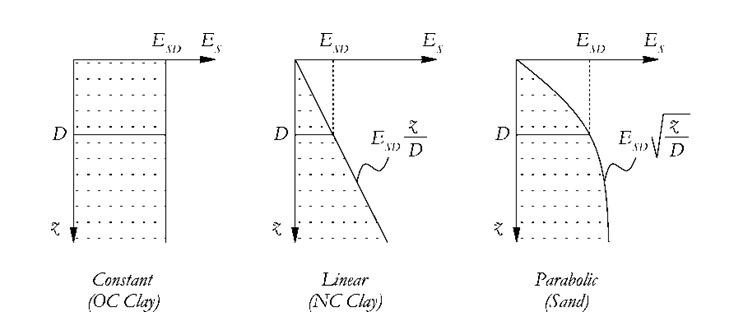
Le espressioni per larigidezza statica del palo sono adattate le espressioni dell’ EC 8 – Part 5 [2003]. con leggere modifiche. Queste si possono ritenere valideper pali flessibili o profondi e sono riassunte nella tabella sottostante
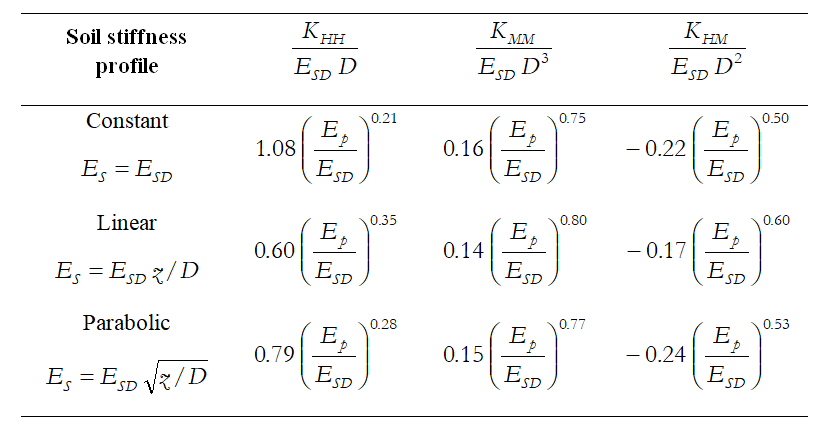
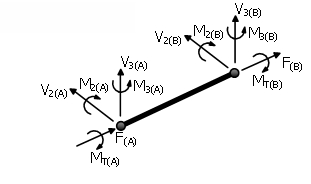
In queste espressioni, D è il diametro del palo, ESD è il modulo di deformazione del terreno alla profondità pari al diametro del palo ed Ep è il modulo di Young del materiale del palo. I termini della matrice di rigidezza del palo seguono la convenzione di segno mostrata nella figura sottostante.

In Gazetas [1991] sono presentati I corrispondenti coefficient di smorzamento, che sono calcolati per ciascuna frequenza f in accordo con le espressioni riportate nella tabella sottostante.
Le componenti dinamiche della rigidezza del palo mostrate in Gazetas [1984] devono essere approssimativamente uguale a uno, per la normale gamma di frequenza di interesse per la risposta strutturale. Quindi, la rigidezza statica del palo può essere utilizzata come quelle dinamiche, per singoli pali flessibili. La variazione delle componenti del rapporto di smorzamento è lineare come previsto dalla tabella sottostante. Ciò significa che, il comportamento dello smorzamento radiale può essere approssimato da dashpot con smorzamento coefficiente di smorzamento costante C.

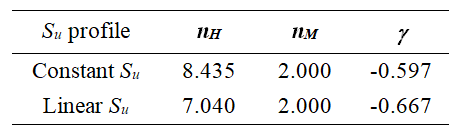
I parametri della bounding surface sono fissati per ciascun profilo di resistenza e sono mostrati nella tabella sottostante. Il valore limite dLim è un parametro correlato alla convergenza numerica e varia tra 0.01 e 0.2, con un valore di default di 0.1.
Infine, I rimanenti 4 parametri di calibrazione, 2 dei quali sono correlati alla risposta monotonica –BETA e PL_H0, e gli altri 2 al comportamento ciclico –ETA e nUR. In alternativa, 2 dei parametri sono relativi al comportamento di “gapping”: –BETA e ETA e gli altri 2 sono legati al modello di plasticità: -PL_H0 e nUR. I parametri BETA, PL_H0 e nUR sono sempre positivi, mentre ETA può essere uguale a zero se non si considera una gap residuo. I valori di default di questi parametri e i rispettivi range di variabilità sono proposti nella tabella sottostante.

Nota
- Si deve prestare attenzione all’input sismico quando si effettua un’analisi dinamica con il macro- element SSI. Infatti, dato che i due nodi del macro-elemento dovrebbero avere lo stesso moto senza alcuna interazione inerziale, il modo più saggio di eseguire l'analisi non è imponendo l’a ccelerogramma nel nodo di base, ma imponendo le corrispondenti forze di inerzia sulle masse strutturali soprastanti.
Assi Locali e Notazioni per l'Output

Alcune basi teoriche sull’analisi di interazione suolo struttura SSI
L’analisi di interazione suolo struttura SSI può essere condotta attraverso l’impiego di un modello non lineare agli elementi finiti solidi (ovvero un soil-block), oppure attraverso un approccio a sottostrutture (macroelemento) più pratico e semplice, che è quello adottato in SeismoStruct.
Quando si modella l’interazione suolo struttura SSI con il metodo delle sottostrutturure, si dovrebbe analizzare innanzitutto l’interazione cinematica dell’intero modello comprensivo sia della struttura che del suolo, considerando la rigidezza strutturale ma non la massa strutturale. In questo metodo, la propagazione dell’input sismico nel terreno è esplicitamente modellata, tipicamente nel dominio delle frequenze (ma non necessariamente), e il risultato finale è l’input di moto della fondazione (foundation input motion FIM), ovvero il moto che avrebbe la fondazione se fosse priva di massa. Questo step iniziale è, tuttavia, spesso tralasciato assumendo che l’interazione cinematica possa essere trascurata e quindi utilizzate il ground motion di campo libero come FIM (questo moto del terreno in campo libero è anche spesso assunto come risultato solo della propagazione verticale delle onde di taglio attraverso uno strato di suolo orizzontale).
Una seconda fase nella modellazione della SSI attraverso una metodologia a sottostruttura dovrebbe tenere in considerazione il calcolo delle impedenze della fondazione (ad es. le proprietà di risposta dinamica della fondazione), tipicamente rappresentate da un set di molle, dashpot (e possibilmente masse fittizie per raggiungere la corretta dipendenza dalla frequenza delle impedenze). Questo secondo step può essere semplificato determinando le impedenze dalle espressioni fornite in letteratura.
Lo step finale è l’analisi della struttura, considerando sia rigidezza che massa, poggiante sulle impedenze di fondazione e soggette a FIM. Questo è quello che è possibile fare in SeismoStruct, che presenta l'ulteriore vantaggio di essere in grado, attraverso l'impiego del macroelemento SSI, di considerare anche la risposta non lineare del sistema di fondazione. In altre parole, un’analisi SSI, svolta impiegando questo macro-elemento corrisponde ad un approccio ibrido tra un’analisi con interazione inierziale dell’approccio a sottostruttrura, che risulta applicabile solamente in caso di risposta lineare, e una modellazione ad elementi finiti solidi non lineari degli effetti della SSI.
Pertanto, in base a quando detto sopra, l'utente deve tenere presente quanto segue:
- Il metodo a sottostruttura è teoricamente corretto solo nel caso di risposta lineare, ad es. senza scorrimento o uplift della fondazione, gapping del palo, degradazione della rigidezza, comportamento plastico, e spostamenti permanenti; in presenza di non linearità, questo tipo di analisi inevitabilmente comporta un certo grado di approssimazione.
- Come si sarà notato, il FIM è l’input di moto che la fondazione avrebbe solo qualora fosse priva di massa (così come il resto della struttura) e se si comportasse in modo lineare. In effetti, e per esempio, se il modello di una fondazione simulasse la sua resistenza allo scorrimento e se ci fosse massa strutturale, il movimento della fondazione non sarebbe più il FIM a causa delle forze inerziali provenienti dalla struttura e da un possibile scorrimento della fondazione. Inoltre, anche nel caso di risposta lineare della fondazione considerando la propria massa (e non quella della struttura soprastante), l’input di moto non sarebbe ancora esattamente il FIM, in quanto si generano forze d inerzia dovute alla massa della fondazione.
- L’input sismico per un’analisi SSI utilizzando l’approccio a sottostruttura (come applicato in SeismoStruct) può essere definito come uno tra i seguenti proposti:
-
- input in accelerazione (time history) al nodo di base vincolato del macro-elemento (questo potrebbe essere il FIM, spesso assunto come equivalente al moto in campo libero, come già discusso), che si propagherà attraverso il macro-elemento e ecciterà le masse strutturali (inclusa quella di fondazione);
- input in forze d’inerzia (time history), calcolate come il prodotto delle masse strutturali (incluse quelle di fondazione) moltiplicate per il FIM, applicato a ciascuna delle masse della struttura.
Questi due approcci di definizione dell'input sismico dovrebbero portare a risultati di analisi identici in termini di spostamenti nodali relativi (e quindi deformazioni / sforzi dei materiali e forze interne degli elementi). Il primo approccio è più semplice da applicare perché si deve definire solo il moto alla base del nodi vincolati. Comunque, questo potrebbe far insorgere problemi di instabilità numerica in casi particolari quando le rigidezze dei macro-elementi sono molto grandi. Il secondo approccio risulta più difficile da applicare, perché si devono applicare forze dinamiche time history a tutti i nodi con massa concentrata e diventa poco agevole quando si usano masse distribuite. Ma questo metodo funziona in tutti i casi.