Macro-elemento Interazione Suolo-Struttura per Fondazioni Superficiali SSI1 -ssilink1

Si tratta di un macro-elemento non lineare per l’interazione suolo-struttura di fondazioni superficiali basato sul lavoro di Correia e Paolucci (2019). Questo approccio a macro-elemento reduce la dimensione del problema in modo significativo, in quanto la fondazione e il suolo sono considerati come un singolo macro-elemento caratterizzato da sei fradi di libertà (6 GDL), nel caso tridimensionale, la cui formulazione è basata sulla risultante delle forze e degli spostamenti. La geometria considerata corrisponde a una Fondazione rigida rettangolare, con accoppiamento tra tutti i GDL del marco-elemento e la loro definizione come elemento link zero-lenght. Considerando per semplicità di notazione e visualizzazione un carico planare, la fondazione sarà soggetta sia a momento flettente (rocking) che ad entrambe le forze verticali e orizzontali (rispettivamente My, N e Hx), come mostrato nella figura sottostante.

 

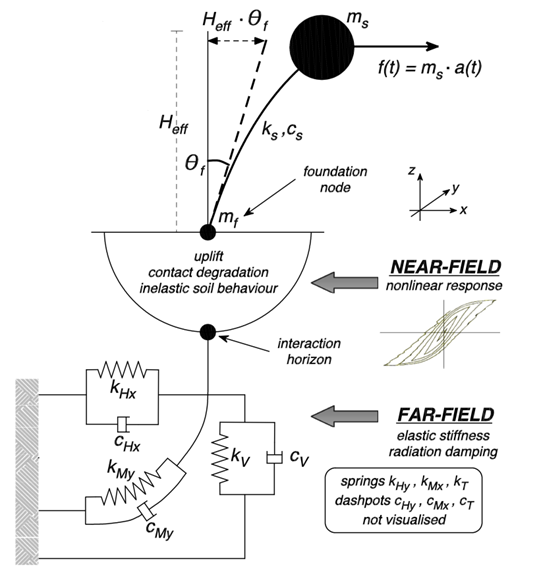
Si impiega un modello di uplift che si basa su una risposta non lineare di uplift-elastico che considera anche alcune degradazioni di contatto all’interfaccia suolo/fondazione dovute a cambiamenti non ripristinabili della geometria. Viene impiegato un modello di plasticità della bounding surface che tiene correttamente in considerazione dell’uplift-elastico e della risposta non lineare plastica. La formulazione di questo macro-elemento è applicabile a condizioni di carico tridimensionali. La figura sottostante rappresenta schematicamente il tipo di fenomeno che si intende modellare con macro-elemento.

Il modello di macro-elemento di fondazione rappresenta il comportamento dinamico di una fondazione rigida isolata, soggetta a carichi inerziali tridimensionali, dalla fase iniziale di carico fino al raggiungimento del collasso. Il macro-elemento si basa su tre principali caratteristiche della risposta delle fondazioni, denominate:

i)      Risposta iniziale elastica,

ii)    Uplift nella risposta a rocking,

iii)  Collasso in condizione di carico.

 

 

Il modello di plasticità della bounding surface è utilizzato per rappresentare la continua transizione tra la risposta inziale elastica e il flusso plastico a rottura, per condizioni di carico monotoniche, cicliche e dinamiche. Il fenomeno di uplift della Fondazione è rappresentato da un modello non lineare elastico che, comunque, tiene in conto ed è influenzato dallo stato di deformazione plastica nello strato di terreno sottostante.

La bounding surface impiegata in questo macro-elemento dipende del tipo di suolo e dalle condizioni di drenaggio durante l’evento sismico. Perciò sono condierate diffenti bounding surface per condizioni drenate e non drenate. La supericie di rottura impiegata per descrivere il comportamento drenato corrisponde alla forma cosiddetta “rugby-ball”, mentre per carico non drenato la superficie di rottura corrisponde alla forma cosidetta “scallop”, che è rappresentata nella figura sottostante in termini di intersezione nei piani di carico H-N e M-N. La forma “rugby-ball” corrisponde ad una superficie di rottura rappresentata dalla linea continua (figura sottostante) in entrambi i piani di carico.

 

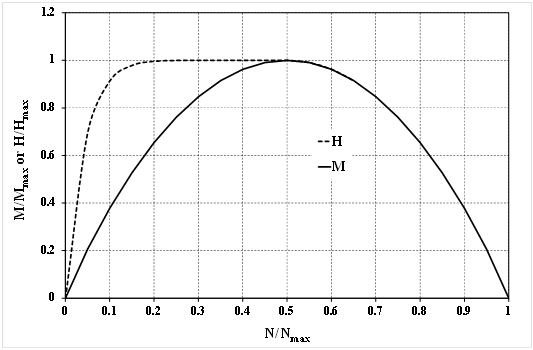
Il macro-elemento richiede la definizione di 25 parametri, dei quali solo 3 necessitano di essere calibrati:

·       le dimensioni della fondazione (lunghezza L e larghezza B);

·       sei componenti della rigidezza iniziale della fondazione, denominate come KN1, KH2, KH3, KM2, KM3, KM2, KTT rispettivamente per direzione verticale, orizzontale e rotazionale, che possono essere valutate utilizzando le formule presenti in letteratura (e.g. Gazetas, 1991) oppure calibrate su risultati di prove sperimentali.

·       la capacità massima di carico verticale concentrato Nmax che corrisponde alla portanza verticale statica della fondazione e può essere valutata con le formule previste dalle normative (e.g. Brinch-Hansen,1970);

·       la capacità massima a taglio Hmax2 and Hmax3 e la capacità a momento alla base Mmax2, Mmax3 , Tmax, che devono essere calibrati basandosi o sulle proprietà del matriale (e.g. angolo di attrito del terreno) o su valori teorici [Butterfield and Gottardi, 1994]

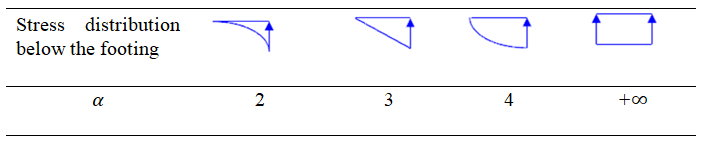
·       il parametro di uplift iniziale α dipende solo dalla distribuzione di sforzi verticali assunta sotto la fondazione e può essere determinato da semplici considerazioni statiche, come mostrato nella tabella sottostante. Non è un parametro che influenza molto i risultati, ed è tipicamente assunto pari a 3, il che corrisponde ad assumere una distribuzione lineare delle sollecitazioni per il suolo all'inizio dell'analisi;

·       L'esponente per la storia di carico in scarico/ricarico nUR , è tipicamente assunto pari a 1, essendo correlato a differenti valori di modulo plastico per scarico/ricarico confrontati con il carico iniziale;

·       il parametro di degrazione del contatto suolo/fondazione, ,tiene in considerazione il decremento dell’area di contatto dovuto all’inelasticità cumulate per rocking e può essere valutato basandosi sui risultati sperimentali;

·       il modulo plastico di riferimento normalizzato, H0pl , calibrato tramite risultati sperimentali;

·       Il parametro potenziale plastico della superficie, , anch’esso calibrato su risultati sperimentali.

Da quanto precede, risulta che, una volta noti i classici parametri elastici e di resistenza per il sistema di fondazione del suolo, rimane un piccolo numero di 3 parametri da calibrare nel processo di validazione:  H0pl  il modulo plastico di riferimento normalizzato, , il parametro potenziale plastico della superficie e , il parametro del modello di danno.

Nota

  1. Dato che il macroelemento SSI presenta una risposta non lineare sin dall'inizio dell'analisi, è molto importante applicare il carico iniziale in più fasi per evitare la mancata convergenza o risultati non esatti. Tipicamente un numero di passi compreso tra 50 e 100 potrebbe essere sufficiente, sebbene in casi più complessi questi potrebbero diventare valori minimi necessari.
  2. Si deve prestare attenzione all’input sismico quando si effettua un’analisi dinamica con il macro- element SSI. Infatti, dato che i due nodi del macro-elemento dovrebbero avere lo stesso moto senza alcuna interazione inerziale, il modo più saggio di eseguire l'analisi non è imponendo l’a ccelerogramma nel nodo di base, ma imponendo le corrispondenti forze di inerzia sulle masse strutturali soprastanti.

Assi Locali e Notazioni per l'Output

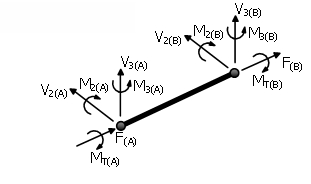
Alcune basi teoriche sull’analisi di interazione suolo struttura SSI

L’analisi di interazione suolo struttura SSI può essere condotta attraverso l’impiego di un modello non lineare agli elementi finiti solidi (ovvero un soil-block), oppure attraverso un approccio a sottostrutture (macroelemento) più pratico e semplice, che è quello adottato in SeismoStruct.

Quando si modella l’interazione suolo struttura SSI con il metodo delle sottostrutturure, si dovrebbe analizzare innanzitutto l’interazione cinematica dell’intero modello comprensivo sia della struttura che del suolo, considerando la rigidezza strutturale ma non la massa strutturale. In questo metodo, la propagazione dell’input sismico nel terreno è esplicitamente modellata, tipicamente nel dominio delle frequenze (ma non necessariamente), e il risultato finale è l’input di moto della fondazione (foundation input motion FIM), ovvero il moto che avrebbe la fondazione se fosse priva di massa. Questo step iniziale è, tuttavia, spesso tralasciato assumendo che l’interazione cinematica possa essere trascurata e quindi utilizzate il ground motion di campo libero come FIM (questo moto del terreno in campo libero è anche spesso assunto come risultato solo della propagazione verticale delle onde di taglio attraverso uno strato di suolo orizzontale).

Una seconda fase nella modellazione della SSI attraverso una metodologia a sottostruttura dovrebbe tenere in considerazione il calcolo delle impedenze della fondazione (ad es. le proprietà di risposta dinamica della fondazione), tipicamente rappresentate da un set di molle, dashpot (e possibilmente masse fittizie per raggiungere la corretta dipendenza dalla frequenza delle impedenze). Questo secondo step può essere semplificato determinando le impedenze dalle espressioni fornite in letteratura.

Lo step finale è l’analisi della struttura, considerando sia rigidezza che massa, poggiante sulle impedenze di fondazione e soggette a FIM. Questo è quello che è possibile fare in SeismoStruct, che presenta l'ulteriore vantaggio di essere in grado, attraverso l'impiego del macroelemento SSI, di considerare anche la risposta non lineare del sistema di fondazione. In altre parole, un’analisi SSI, svolta impiegando questo macro-elemento corrisponde ad un approccio ibrido tra un’analisi con interazione inierziale dell’approccio a sottostruttrura, che risulta applicabile solamente in caso di risposta lineare, e una modellazione ad elementi finiti solidi non lineari degli effetti della SSI.

Pertanto, in base a quando detto sopra, l'utente deve tenere presente quanto segue:

  1. Il metodo a sottostruttura è teoricamente corretto solo nel caso di risposta lineare, ad es. senza scorrimento o uplift della fondazione, gapping del palo, degradazione della rigidezza, comportamento plastico, e spostamenti permanenti; in presenza di non linearità, questo tipo di analisi inevitabilmente comporta un certo grado di approssimazione.
  2. Come si sarà notato, il FIM è l’input di moto che la fondazione avrebbe solo qualora fosse priva di massa (così come il resto della struttura) e se si comportasse in modo lineare. In effetti, e per esempio, se il modello di una fondazione simulasse la sua resistenza allo scorrimento e se ci fosse massa strutturale, il movimento della fondazione non sarebbe più il FIM a causa delle forze inerziali provenienti dalla struttura e da un possibile scorrimento della fondazione. Inoltre, anche nel caso di risposta lineare della fondazione considerando la propria massa (e non quella della struttura soprastante), l’input di moto non sarebbe ancora esattamente il FIM, in quanto si generano forze d inerzia dovute alla massa della fondazione.
  3. L’input sismico per un’analisi SSI utilizzando l’approccio a sottostruttura (come applicato in SeismoStruct) può essere definito come uno tra i seguenti proposti:
    • input in accelerazione (time history) al nodo di base vincolato del macro-elemento (questo potrebbe essere il FIM, spesso assunto come equivalente al moto in campo libero, come già discusso), che si propagherà attraverso il macro-elemento e ecciterà le masse strutturali (inclusa quella di fondazione);
    • input in forze d’inerzia (time history), calcolate come il prodotto delle masse strutturali (incluse quelle di fondazione) moltiplicate per il FIM, applicato a ciascuna delle masse della struttura.

Questi due approcci di definizione dell'input sismico dovrebbero portare a risultati di analisi identici in termini di spostamenti nodali relativi (e quindi deformazioni / sforzi dei materiali e forze interne degli elementi). Il primo approccio è più semplice da applicare perché si deve definire solo il moto alla base del nodi vincolati. Comunque, questo potrebbe far insorgere problemi di instabilità numerica in casi particolari quando le rigidezze dei macro-elementi sono molto grandi. Il secondo approccio risulta più difficile da applicare, perché si devono applicare forze dinamiche time history a tutti i nodi con massa concentrata e diventa poco agevole quando si usano masse distribuite. Ma questo metodo funziona in tutti i casi.