Numerical instability, divergence and iteration prediction
In addition to the convergence verification, at the end of an iterative step three other solution checks may be carried out; numerical instability, solution divergence and iteration prediction. These criteria, all of a force/moment nature, serve the purpose of avoiding the computation of useless equilibrium iterations in cases where it is apparent that convergence will not be reached, thus minimising the duration of the analysis.
Numerical instability
The possibility of the solution becoming numerically unstable is checked at every iteration by comparing the Euclidean norm of out-of-balance loads, Gnorm, with a pre-defined maximum tolerance (default=1.0E+20), several orders of magnitude larger than the applied load vector. If Gnorm exceeds this tolerance, then the solution is assumed as being numerically unstable and iterations within the current increment are interrupted, with a log flag message equal to Max_Tol.
On occasions, very unstable models lead to the sudden development of out-of-balance forces that are several orders of magnitude larger than the maximum tolerance value. This in turn creates a so-called Solution Problem (i.e. the analysis crashes, albeit in a "clean manner"), and iterations within the current increment are interrupted, with a log flag message equal to Sol_Prb.
Solution divergence
Divergence of the solution is checked by comparing the value of Gnorm obtained in the current iteration with that obtained in the previous one. If Gnorm has increased, then it is assumed that the solution is diverging and iterations within the current increment are interrupted, with a log flag message equal to Diverge.
Iteration prediction
Finally, a logarithmic convergence rate check is also carried out, so as to try to predict the number of iterations (itepred) required for convergence to be achieved. If itepred is larger than the maximum number of iterations specified by the user, then it is assumed that the solution will not achieve convergence and iterations within the current increment are interrupted, with a log flag message equal to Prd_Ite.
The following equation is used to compute the value of itepred, noting that ite represents the current number of iterations and Gtol is the force/moment tolerance:
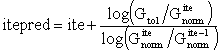
The three checks described above are usually reliable and effective within the scope of applicability of SeismoStruct, for as long as the divergence and iteration prediction check is not carried out during the first iterations of an increment when the solution might not yet be stable enough. This issue is discussed in further detail in the iterative strategy section, where all user-defined parameters related to these criteria are described.
Note: Some element types (infrmFB, infrmFBPH, infrmDBPH & masonry) require a number of iterations to be carried in order for internal equilibrium to be reached. In some cases, the latter element loop equilibrium cannot be reached, as signalled by log flag messages elm_inv and elm_ite. Refer to here for further information on this issue.