Convergence criteria

Four different convergence check schemes, which make use of two distinct criteria (displacement/rotation and force/moment based), are available in SeismoStruct for checking the convergence of a solution at the end of every iteration:

a. Displacement/Rotation based scheme
b. Force/Moment based scheme
c. Displacement/Rotation AND Force/Moment based scheme
d. Displacement/Rotation OR Force/Moment based scheme

Herein, the formulation of the two criteria employed in all four schemes is given, whilst the applicability of the latter is discussed elsewhere.

The displacement/rotation criterion consists in verifying, for each individual degree-of-freedom of the structure, that the current iterative displacement/rotation is less or equal than a user-specified tolerance. In other words, if and when all values of displacement or rotation that result from the application of the iterative (out-of-balance) load vector are less or equal to the pre-defined displacement/rotation tolerance factors, then the solution is deemed as having converged. This concept can be mathematically expressed in the following manner:

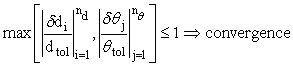
The force/moment criterion, on the other hand, comprises the calculation of the Euclidean norm of the iterative out-of-balance load vector (normalised to the incremental loads), and subsequent comparison to a user-defined tolerance factor. It is therefore a global convergence check (convergence is not checked for every individual degree-of-freedom as is done for the displacement/rotation case) that provides an image of the overall state of convergence of the solution, and which can be mathematically described in the following manner:

Note: The use of a global, as opposed to local, force/moment criterion is justified with the fact that, in SeismoStruct, it is common for load vectors to feature significant variations in the order of magnitude of forces/moments applied at different degrees-of-freedom of the structure, particularly in the cases where infinitely stiff/rigid connections are modelled with link elements. Hence, the employment of a local criterion, as is done in the case of displacement/rotation criterion, would lead to over-conservative and difficult-to-verify converge checks.