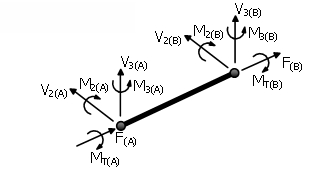
Elemento Inelástico de Mampostería – masonry

Este elemento es una combinación de un tipo de elemento de rótula plástica en 3D y de formulación basada en la fuerza, empleado en el modelado principalmente del comportamiento de flexión del miembro de mampostería (mencionado aquí como el 'subelemento interno') con dos links en los dos extremos que se emplean para simular el comportamiento de corte del miembro (denominados "links externos" o "subelementos de link"). El subelemento interno y los links externos están conectados en serie, asegurando el equilibrio en el momento flector y la fuerza de corte. Los únicos grados de libertad 'activos' de los subelementos de link son los dos traslacionales en las direcciones de corte (en el plano y fuera del plano), mientras que los otros cuatro DOF (axial y 3 rotacional) permanecen perfectamente links rígidos. Los muros de mampostería y los antepechos se pueden modelar con precisión con esta configuración.

Los DOF de corte de los subelementos de tipo link presentan una curva histerética que se basa en la curva no lineal MIMK_bilin incorporada de SeismoStruct (curva de deterioro modificada Ibarra-Medina-Krawinkler con bilineales reglas de histéresis), de acuerdo con una ley que describe el comportamiento de corte de todo el miembro Simultáneamente, en el subelemento interno, el modelado de la sección de fibra permite una descripción relativamente precisa del comportamiento de flexión axial acoplada. El estado de tensión-deformación seccional se obtiene a través de la integración de la respuesta de material uniaxial no lineal de las fibras individuales, en las que la sección se ha subdividido, lo que explica completamente la propagación de la inelasticidad a lo largo de la longitud del miembro y a través de la profundidad de la sección (como se describe en la sección de la Inelasticidad de Material).

La determinación de la resistencia al corte del miembro es crucial en la precisión del modelo, y el modelo la lleva a cabo automáticamente, en función de las propiedades del material de mampostería, las dimensiones del miembro y el Código estructural seleccionado. Las siguientes expresiones se emplean para el cálculo de la capacidad de corte del miembro (se observa que se emplean diferentes ecuaciones en los diferentes estándares).

• En el Eurocódigo 8, se emplea el mecanismo de falla del deslizamiento de la junta horizontal:

• En ASCE 41-17 y para muros URM de mampostería no reforzadas, se utiliza el valor más bajo de la resistencia al deslizamiento de la junta horizontal y la resistencia a la tensión diagonal, de acuerdo con las siguientes expresiones:

 

• En ASCE 41-17 y para los antepechos URM de mampostería no reforzada, se utiliza el valor más bajo de la resistencia de la junta de la cama y la resistencia a la tensión diagonal, de acuerdo con las siguientes expresiones:

• En ASCE 41-17 y para muros de mampostería o antepechos con refuerzo, se emplea la siguiente expresión:

• En NTC-18 y para los antepechos URM de mampostería no reforzada se utilizan diferentes expresiones para los diferentes tipos de materiales: (i) para mampostería con bloques se emplea el criterio de Mohr-Coulomb, (ii) para mampostería con ladrillos o piedras regulares, la resistencia es igual al valor más bajo de los criterios de Turnšek y Čačovič y de Mann y Müller y (iii) para mampostería con piedras irregulares se emplea la expresión de Turnšek y Čačovič.

Mohr-Coulomb(§7.8.2.2.2 NTC-18 y  §6.2 EC6):  

Turnšek-Čačovič (§C8.7.1.3.1.1 Comentario de NTC-18):  

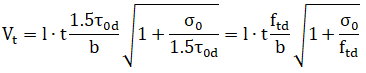
Mann-Müller (§C8.7.1.3.1.1 Comentario de NTC-18):           

• En NTC-18 y para mampostería reforzada RM, la capacidad de corte se calcula de acuerdo con §7.8.3.2.2 NTC2018:

Nota: en las revisiones de acuerdo con KANEPE se emplean las expresiones de EC8. De manera similar, con TBDY se usan las ecuaciones ASCE 41. Para obtener una descripción completa de las expresiones empleadas en cada Norma, los usuarios pueden consultar los Apéndices H1 a H6.

Se pueden usar dos modelos especiales de material de mampostería con el tipo de elemento de mampostería, mas_par y mas_tl. El primero se basa en el modelo de material de hormigón con_ma, mientras que el segundo es un modelo multilineal más simple con degradación y resistencia residual. Ambos modelos presentan parámetros, tales como la resistencia a la compresión, la resistencia al corte y la resistencia a la tracción, que se emplean en la determinación de la resistencia al corte del miembro. Del mismo modo, hay dos tipos de secciones específicas de mampostería en SeismoStruct, la mws para muros de mampostería y la mss  para antepechos. Tanto los miembros de mampostería URM no reforzada como los miembros de mampostería RM reforzada se pueden modelar efectivamente con las características propuestas.

Nota: El tipo de elemento de mampostería solo se puede usar con los modelos de material mas_par y mas_tl. De manera similar, solo se pueden emplear los tipos de secciones especiales de mampostería mws y mss. La razón de esto es que pueden almacenar parámetros que se utilizan para el cálculo automático de la resistencia al corte del miembro.

Los usuarios pueden elegir si calcular la resistencia al corte de la mampostería (i) solo en el paso inicial, (ii) en todos los pasos hasta la fluencia del corte o (iii) en cada paso, es decir, incluso después de alcanzar la capacidad máxima del miembro. La opción predeterminada es la segunda, que es actualizar la resistencia al corte hasta el rendimiento, que es la mejor combinación de precisión y estabilidad, ya que actualizar la resistencia al corte en la rama descendente de la curva de capacidad puede conducir a dificultades de convergencia sin mejorar significativamente la precisión de la solución

Los parámetros necesarios para la definición completa de las propiedades del elemento son los siguientes:

 

• El número de fibras de la sección utilizadas en los cálculos de equilibrio realizados en cada una de las secciones de integración del subelemento interno.

• La reducción de la rigidez elástica α es la reducción de la rigidez elástica no agrietada de la curva de deformación por fuerza de corte que se emplea en los cálculos

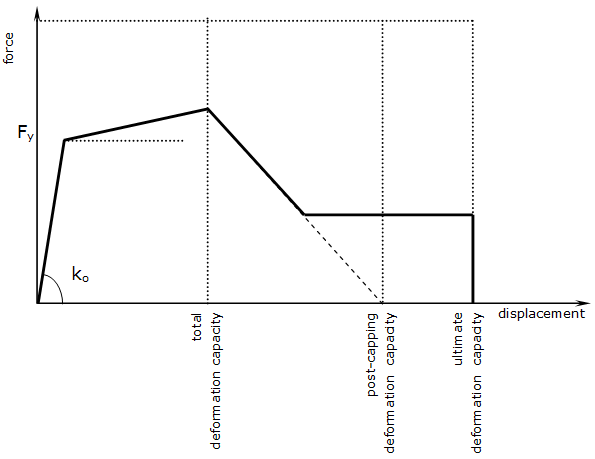
• La capacidad total de deformación por corte, que es la capacidad de deformación final del miembro d_tot = d_yield + d_plastic. Se observa que la deformación de fluencia d_yield se calcula directamente por el programa a partir de la rigidez al corte elástico y la resistencia a la deformación.

• La capacidad de deformación post-capping por corte: este es el nivel de deformación, en el cual la extrapolación de la rama descendente de la curva de deformación por fuerza de corte alcanza el eje cero.

• La capacidad de deformación de corte última: este es el nivel de deformación, después del cual no hay resistencia residual  

• La razón de resistencia al corte residual es la relación entre la resistencia máxima (en el nivel de capacidad de deformación total) y la resistencia residual

• La razón de endurecimiento por deformación por corte es la relación entre las ramas elástica y plástica de la curva de fuerza-deformación por corte

• Los parámetros de deterioro cíclico para la resistencia al corte y la rigidez son los siguientes tres parámetros: (i) el parámetro de deterioro cíclico para el deterioro de la resistencia - Λs, (ii) el parámetro de deterioro cíclico para el deterioro de la rigidez de descarga - ΛK, y (iii) el parámetro  cíclico de deterioro para el deterioro de la resistencia post-capping - Λc. Para todos los parámetros, cuanto menor es el factor, mayor es el deterioro impuesto en la curva, sin embargo, debe notarse que un valor cero no conduce a ningún deterioro. Para obtener una descripción completa de los parámetros, consulte la documentación de la curva MIMK_bilin

• Razón entre la fuerza al inicio de la recarga y la fuerza correspondiente a la deformación máxima experimentada para las direcciones de carga positiva y negativa.

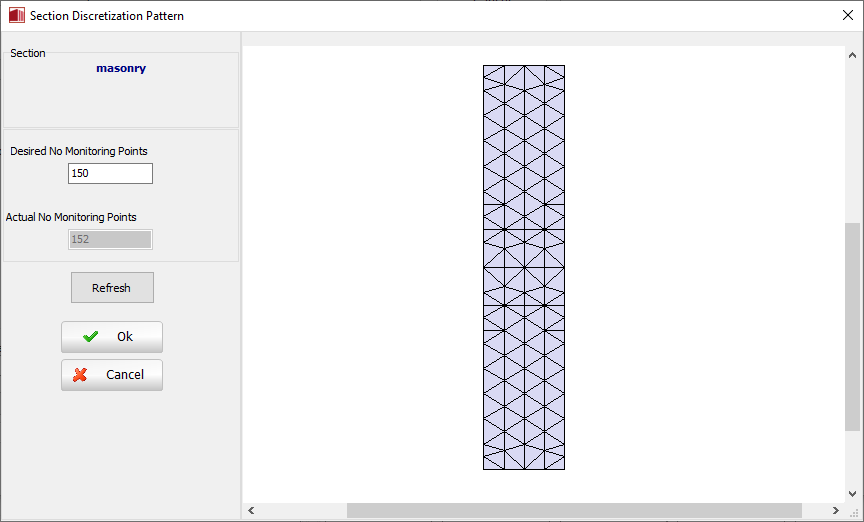
Con respecto a las fibras de sección, el número ideal, suficiente para garantizar una reproducción adecuada de la distribución de tensión-deformación a través de la sección del elemento, varía con la forma y las características del material de el elemento, y el grado de inelasticidad a la que el elemento será forzado a. Como regla general, los usuarios pueden considerar que generalmente 100 fibras deberían ser adecuadas.

En el cuadro de diálogo Esquema de Discretización de la Sección, el software proporciona el número deseado y real (después de que se haya realizado la discretización de sección, empleando procedimientos de triangulación) de puntos de monitoreo que se emplearán en el análisis. Al hacer clic en el botón Actualizar, es posible actualizar la vista de la sección de discretización.  

De manera similar a los tipos de elementos de marco inelásticos, en lugar de discretizar los elementos para representar los cambios en los detalles de refuerzo, es posible usar un solo elemento por miembro y luego definir múltiples secciones dentro del elemento. Se observa que estas secciones pueden diferir solo en el refuerzo (es decir, el tipo de sección, las dimensiones y los materiales deben ser los mismos).

En el cuadro de diálogo de este elemento también es posible definir una amortiguación específica del elemento, en oposición a la amortiguación global definida aquí. Para hacerlo, los usuarios simplemente tienen que presionar el botón Amortiguación y luego seleccionar el tipo de amortiguación que mejor se adapte al elemento en cuestión (los usuarios deben consultar el menú Amortiguación para una discusión sobre los diferentes tipos de amortiguación disponibles y sugerencias sobre cuáles podrían mejores opciones). El amortiguamiento definido a nivel de los elementos prevalece por sobre el amortiguamiento global, es decir, los coeficientes de la matriz de amortiguamiento calculados "a nivel global" asociados a los grados de libertad de un elemento dado serán reemplazados por los coeficientes calculados a través del producto de la matriz de masa del elemento y un parámetro proporcional a la masa, o a través del producto de la matriz de rigidez del elemento y un parámetro proporcional a la rigidez, o mediante el cálculo de una matriz de amortiguamiento de Rayleigh del elemento.

Nota: Si se define amortiguamiento de Rayleigh a nivel del elemento utilizando coeficientes diferentes para distintos elementos o respecto de aquellos empleados en los ajustes de amortiguamiento global, entonces se está modelando un amortiguamiento de Rayleigh "no-clásico", ya que el amortiguamiento de Rayleigh "clásico" requiere la definición de coeficientes uniformes.

Ejes Locales y Notación del Output