Amortiguamiento
En los análisis dinámicos no lineales, el amortiguamiento histerético, que es habitualmente responsable de la disipación de la mayoría de la energía sísmica, se encuentra incluido implícitamente en la formulación del modelo con fibras no lineales de los elementos inelásticos de pórtico (infrm, infrmPH) o dentro de la curva de respuesta fuerza-desplazamiento no lineal utilizada para caracterizar la respuesta de los elementos link. Existe, sin embargo, una cantidad relativamente pequeña de amortiguamiento no histerético que es también movilizado durante la respuesta dinámica de las estructuras, a través de fenómenos como la fricción entre elementos estructurales y no estructurales, fricción en las fisuras abiertas del concreto, radiación de energía a través de las fundaciones, etc., y que puede no haber sido modelado en el análisis. Tradicionalmente, dichas fuentes modestas de disipación energética han sido consideradas mediante el uso del amortiguamiento de Rayleigh [por ej., Clough and Penzien, 1993; Chopra, 1995] con valores de amortiguamiento viscoso equivalente (x) de entre 1% y 8%, dependiendo de la tipología estructural, los materiales utilizados, los elementos no estructurales, el período y magnitud de la vibración, el modo de vibración considerado, etc. [por ej., Wakabayashi, 1986].
Existe cierto grado de desacuerdo en la comunidad científica/ingenieril respecto del uso del amortiguamiento viscoso equivalente para representar fuentes de disipación de energía que no se encuentren incluidos explícitamente en el modelo. De hecho, algunos autores [por ej., Wilson, 2001] sugieren fuertemente evitar todo uso del mismo, mientras que otros [Priestley and Grant, 2005; Hall, 2006] recomiendan su uso pero no mediante el amortiguamiento de Rayleigh, que es proporcional tanto a la rigidez como a la masa, sino a través del uso de amortiguamiento proporcional a la rigidez solamente; como es descrito por Pegon [1996], Wilson [2001], Abbasi et al. [2004] y Hall [2006], entre otros, si una estructura dada es "insensible" al movimiento de cuerpo rígido, el amortiguamiento proporcional a la masa genera disipación energética espuria (es decir, irreal). El enfoque de modelado del amortiguamiento proporcional a la rigidez puede ser subdividido, a su vez, en amortiguamiento proporcional a la rigidez inicial y amortiguamiento proporcional a la rigidez tangencial, siendo este último posiblemente la opción más sólida para las estructuras comunes, como ha sido demostrado por Priestley and Grant [2005].
Sin embargo, incluso si uno pudiese incluir todas las fuentes de disipación energética en un modelo de elementos finitos dado, es decir, modelar explícitamente los paneles divisorios, dispositivos discipativos, la interacción suelo-estructura, etc. (lo cual es, sin lugar a dudas, la mejor opción), la introducción de una cantidad muy pequeña de amortiguamiento viscoso equivalente puede resultar altamente beneficiosa para la estabilidad numérica de análisis dinámicos altamente inelásticos, dado que la matriz de amortiguamiento viscoso tiene un efecto "estabilizador" en el sistema de ecuaciones. Por lo tanto, su uso es generalmente recomendado, aunque con valores suficientemente pequeños. En la ventana de diálogo de Amortiguamiento, los usuarios pueden escoger (i) no usar amortiguamiento viscoso, (ii) utilizar amortiguamiento proporcional a la rigidez, (iii) introducir amortiguamiento proporcional a la masa o, (iv) utilizar el amortiguamiento de Rayleigh.
Amortiguamiento proporcional a la Rigidez
Para el amortiguamiento proporcional a la rigidez, el usuario debe especificar el valor del multiplicador de la matriz de rigidez (aK) que desea utilizarTípicamente, aunque no de manera exclusiva, dicho valor es calculado utilizando la siguiente ecuación:
![]()
Amortiguamiento proporcional a la Masa
Para el amortiguamiento proporcional a la masa, el usuario debe especificar el valor del multiplicador de la matriz de masa (aM) que desea utilizar. Típicamente, aunque no de manera exclusiva, dicho valor es calculado utilizando la siguiente ecuación:
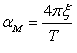
Amortiguamiento de Rayleigh
Para el amortiguamiento de Rayleigh, el usuario debe especificar los valores del período (T) y amortiguamiento (![]() ) del primer y último modo de interés (llamados aquí modo 1 y 2). Los multiplicadores de la matriz de masa (
) del primer y último modo de interés (llamados aquí modo 1 y 2). Los multiplicadores de la matriz de masa (![]() ) y rigidez (
) y rigidez (![]() ) son calculados por el programa, utilizando las expresiones dadas a continuación, que aseguran que el verdadero amortiguamiento de Rayleigh sea obtenido (si se utilizaran coeficientes definidos arbitrariamente, se estaría empleando, en efecto, amortiguamiento matricial en lugar de amortiguamiento de Rayleigh):
) son calculados por el programa, utilizando las expresiones dadas a continuación, que aseguran que el verdadero amortiguamiento de Rayleigh sea obtenido (si se utilizaran coeficientes definidos arbitrariamente, se estaría empleando, en efecto, amortiguamiento matricial en lugar de amortiguamiento de Rayleigh):
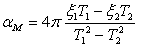 y
y 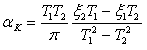
Notas
- El valor de la matriz de amortiguamiento proporcional a la rigidez tangencial es actualizado con cada incremento de carga, no en cada iteración, ya que esto ocasionaría mayor inestabilidad numérica y aumento del tiempo de ejecución.
- Si surgieran dificultades numéricas por el uso del amortiguamiento proporcional a la rigidez tangencial, se recomienda al usuario utilizar entonces amortiguamiento proporcional a la rigidez inicial, utilizando un coeficiente de amortiguamiento viscoso equivalente reducido, a fin de evitar la introducción de efectos de amortiguamiento viscoso exageradamente elevados. En otras palabras, mientras un amortiguamiento viscoso del 2-3% puede ser una suposición razonable para una estructura de concreto armado que haga uso del amortiguamiento proporcional a la rigidez tangencial, un valor mucho menor (0.5-1%) debe ser especificado si se utiliza, en cambio, el amortiguamiento proporcional a la rigidez inicial.
- Las fuerzas de amortiguamiento en modelos que presenten elementos con una rigidez muy elevada (por ej., puentes con estribos rígidos, edificios con muros rígidos, etc.) pueden resultar irreales - el amortiguamiento general en el modelo de un puente puede introducir fuerzas de amortiguamiento significativas, debido, por ejemplo, a la elevada rigidez de los estribos.
- Existe una amplia variedad de tipos de amortiguamiento matricial que son utilizados en diferentes programas de elementos finitos. Estas variaciones pueden presentar ventajas respecto al tradicional amortiguamiento de Rayleigh (por ejemplo, la reducción del nivel de amortiguamiento introducido en los modos altos, etc). Sin embargo, consideramos que dicho nivel de refinamiento no es necesariamente requerido por la mayoría de los análisis, razón por la cual sólo las tres modalidades de amortiguamiento viscoso presentadas anteriormente se encuentran disponibles en SeismoStruct.
- Existe una dispersión significativa en las diferentes propuestas respecto a los valores efectivos de amortiguamiento viscoso equivalente a ser utilizados en la ejecución de análisis dinámicos, por lo que se recomienda al usuario investigar en profundidad este asunto con el fin de determinar los valores más adecuados para su análisis en particular. Éstos dependen del tipo de material (típicamente, se utilizan mayores valores para el concreto que para el acero, por ejemplo), configuración estructural (un pórtico de varios pisos con paneles divisorios/de cerramiento puede presentar valores mayores que una pila de un puente de un solo GDL), nivel de deformación (para bajos niveles de deformación, puede resultar justificable la utilización de valores de amortiguamiento viscoso equivalente mayores que aquellos utilizados en análisis en los que los edificios son llevados hasta altos niveles de respuesta inelástica, dado que es probable que en este último caso la contribución de los elementos no estructurales resulte de menor importancia, por ejemplo), estrategia de modelado (por ejemplo, en el modelado con fibras la fisuración es tenida en cuenta en forma explícita y, por ende, no necesita ser representada mediante el amortiguamiento viscoso equivalente, como en el caso del modelado con plasticidad concentrada utilizando relaciones bi-lineales de momento-curvatura).