Inelasticidad de los Materiales
El uso de elementos con inelasticidad distribuida está comenzando a ser cada vez más habitual en aplicaciones de ingeniería sísmica, tanto en investigación como en el ejercicio profesional. Dado que autores como Filippou and Fenves [2004] o Fragiadakis and Papadrakakis [2008] brindan un tratamiento exhaustivo de sus ventajas en relación con los modelos más simples de plasticidad concentrada, así como también una descripción concisa de su evolución histórica y sus limitaciones, aquí simplemente se hará mención del hecho de que los elementos con inelasticidad distribuida no requieren de la calibración (no siempre directa) de parámetros empíricos de respuesta a partir de la respuesta real o ideal de un elemento de pórtico bajo condiciones de carga ideales, como es el caso para los modelos de plasticidad concentrada.
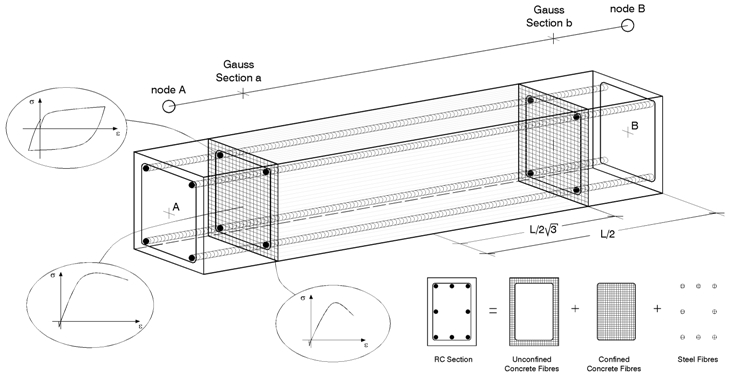
En SeismoStruct se hace uso del llamado "enfoque de fibras" para representar el comportamiento de las secciones transversales, donde cada fibra es asociada a una relación uniaxial esfuerzo-deformación; el estado seccional de esfuerzo-deformación de los elementos viga-columna es obtenido mediante la integración de la respuesta esfuerzo-deformación uniaxial no lineal de las fibras individuales (típicamente 100-150) en las cuales ha sido subdividida la sección (en la figura de abajo se esquematiza, a modo de ejemplo, la discretización de una sección transversal típica de concreto armado).
Este tipo de modelos presenta numerosas ventajas adicionales, las cuales pueden resumirse en: (i) no es necesario realizar análisis momento-curvatura previos para definir los elementos; (ii) no es necesario definir ningún tipo de respuesta histerética de los elementos (dado que queda definida implícitamente mediante los modelos constitutivos de los materiales); (iii) modelado directo de la interacción entre esfuerzo axial y momento flector (tanto para la resistencia como para la rigidez); (iv) representación directa de la carga biaxial y de la interacción de la resistencia flexional en direcciones ortogonales.
Los elementos de pórtico con inelasticidad distribuida pueden ser implementados mediante dos formulaciones de elementos finitos (FE) diferentes: la clásica formulación basada en desplazamientos ("DB", displacement-based) [por ej., Hellesland and Scordelis 1981; Mari and Scordelis 1984], y la más reciente formulación basada en fuerzas ("FB", force-based) [por ej., Spacone et al. 1996; Neuenhofer and Filippou 1997]. En el enfoque DB, el campo de desplazamientos es impuesto, mientras que en un elemento FB el equilibrio es satisfecho estrictamente y no se aplican restricciones al desarrollo de deformaciones inelásticas a lo largo del miembro; por mayores detalles ver, por ej., Alemdar and White [2005] y Freitas et al. [1999].
En el enfoque DB se utilizan funciones de forma de desplazamientos que corresponden, por ejemplo, a una variación lineal de la curvatura del elemento. Para el caso DB, en cambio, una variación lineal de momento es impuesta, es decir, la contraparte de la variación lineal de la curvatura. Cuando el comportamiento del material es elástico y lineal, ambos enfoques producen, naturalmente, el mismo resultado, a condición de que sólo actúen fuerzas nodales sobre el elemento. Por el contrario, cuando el material presenta comportamiento inelástico, la imposición de un campo de desplazamientos no permite capturar la forma deformada real dado que el campo de curvaturas puede ser, para el caso general, altamente no lineal. En esta situación, si se utiliza una formulación basada en desplazamientos es necesario realizar una discretización (meshing) refinada del elemento estructural (típicamente 4-5 elementos por cada miembro estructural) para el cálculo de los desplazamientos/fuerzas nodales, para poder aceptar la hipótesis de un campo lineal de curvaturas dentro de cada sub-dominio. Aún así, se recomienda a los usuarios no utilizar los valores de curvatura seccional y estados esfuerzo-deformación de fibras individuales calculados de esta forma.
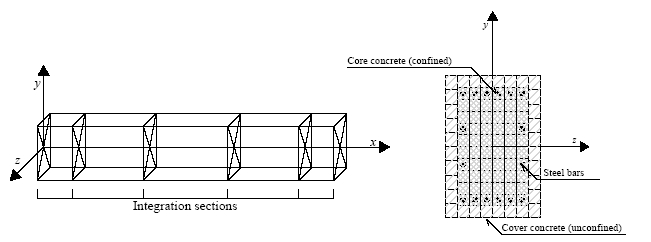
Por el contrario, la formulación basada en fuerzas es siempre exacta, dado que no depende del comportamiento constitutivo que se asuma para la sección. De hecho, no restringe de ninguna manera el campo de desplazamientos del elemento. En este sentido, esta formulación puede ser considerada "exacta", siendo el número discreto de secciones de control utilizadas para la integración numérica a lo largo del elemento la única aproximación introducida. Un mínimo de 3 secciones de integración Gauss-Lobatto son necesarias para evitar una sub-integración, aunque dicha opción no podrá, en general, simular la difusión de la inelasticidad en forma aceptable. Consecuentemente, el número mínimo sugerido de puntos de integración (IP) es 4, aunque suelen utilizarse típicamente entre 5 y 7 (ver figura abajo). Esto permite el modelado de cada miembro estructural con un sólo elemento finito, permitiendo así una correspondencia biunívoca (one-to-one) entre miembros estructurales (vigas y columnas) y elementos del modelo. En otras palabras, al utilizar elementos con formulación FB no es necesario, en teoría, discretizar el elemento, incluso si la sección transversal no es constante. Esto es así debido a que el campo de fuerzas es siempre exacto, independientemente del nivel de inelasticidad.
En SeismoStruct se encuentran implementadas las dos formulaciones descritas (DB y FB). Sin embargo, la formulación basada en fuerzas es típicamente recomendada dado que, como se mencionó anteriormente, no requiere (en general) de la discretización de los elementos, dando lugar así a modelos considerablemente más pequeños (en comparación a aquellos en los que se utiliza la formulación DB) y, por lo tanto, análisis mucho más rápidos, a pesar de que los elementos FB requieran cálculos de equilibrio computacionalmente más demandantes. Una excepción a lo dicho respecto de la no discretización surge cuando se prevén efectos de localización, en cuyo caso es necesario tomar precauciones/medidas especiales, como se describe en Calabrese et al. [2010].
Por otra parte, el uso de un solo elemento por cada miembro estructural permite a los usuarios utilizar el output de rotaciones de cuerda de los elementos para llevar a cabo verificaciones según las normativas (por ej. según Eurocódigo 8, FEMA-356, ATC-40, etc). Por el contrario, cuando el miembro estructural debe ser discretizado en dos o más elementos de pórtico (necesariamente el caso para los elementos DB), los usuarios deben realizar un post-procesado de los desplazamientos/rotaciones nodales para poder estimar las rotaciones de cuerda de los elementos (por ej., Mpampatsikos et al. 2008).
Finalmente, debe notarse que, con el fin de obtener una mayor precisión, en SeismoStruct se utiliza la cuadratura de Gauss-Legendre para los elementos DB (los cuales hacen uso de dos secciones de integración) y la cuadratura de Gauss-Lobatto para los elementos FB (para los cuales se emplean de 4 a 10 secciones de integración). Si bien los usuarios pueden referirse a la literatura (o a esta fuente en línea) por mayores detalles sobre dichas reglas, se dan a continuación las coordenadas aproximadas a lo largo del elemento (medidas desde su baricentro) de las secciones de integración:
- 2 secciones de integración: [-0.577 0.577] x L/2
- 3 secciones de integración: [-1 0.0 1] x L/2
- 4 secciones de integración: [-1 -0.447 0.447 1] x L/2
- 5 secciones de integración: [-1 -0.655 0.0 0.655 1] x L/2
- 6 secciones de integración: [-1 -0.765 -0.285 0.285 0.765 1] x L/2
- 7 secciones de integración: [-1 -0.830 -0.469 0.0 0.469 0.830 1] x L/2
- 8 secciones de integración: [-1 -0.872 -0.592 -0.209 0.209 0.592 0.872 1] x L/2
- 9 secciones de integración: [-1 -0.900 -0.677 -0.363 0.0 0.363 0.677 0.900 1] x L/2
- 10 secciones de integración: [-1 -0.920 -0.739 -0.478 -0.165 0.165 0.478 0.739 0.920 1] x L/2
Notas
- Con la formulación basada sobre fuerzas es inmediatamente posible tener en cuenta las fuerzas que actúan a lo largo del miembro, mientras que en el enfoque DB las cargas distribuidas deben ser transformadas en fuerzas/momentos equivalentes en los nodos extremos del elemento (y luego es necesario utilizar una larga operación de recuperación de los esfuerzos para determinar las solicitaciones correctas en los elementos). Sin embargo, la posibilidad de introducir explícitamente cargas distribuidas no ha sido implementada aún en SeismoStruct, por lo cual el programa siempre aplicará cargas puntuales en los extremos de los elementos.
- Si el usuario lo desea, es posible también implementar un enfoque de plasticidad concentrada en SeismoStruct, en contraposición a la filosofía de modelado con plasticidad distribuida intrínseca de los elementos disponibles en el programa. Esto es posible utilizando el elemento elástico de pórtico (elfrm) en conjunto con links no lineales ubicados en sus extremos (alternativamente, es posible utilizar el elemento inelástico de pórtico con rótula plástica (infrmFBPH) que, si bien presenta una formulación de inelasticidad distribuida basada en fuerzas, permite concentrar dicha inelasticidad en una longitud determinada del elemento). Este enfoque de modelado (plasticidad concentrada) debe, sin embargo, ser utilizado con precaución, dado que la precisión del análisis puede verse comprometida si los usuarios no poseen experiencia suficiente en la calibración de las curvas de respuesta disponibles (a utilizar para la caracterización de los elementos tipo link), con cuyos grados de libertad desacoplados por naturaleza no es posible modelar las curvas/superficies de interacción de fuerza axial y momento flector.
- Por otro lado, como se mencionó anteriormente, el modelado con inelasticidad distribuida no requiere de experiencia avanzada, dado que el usuario sólo debe introducir las características geométricas y de los materiales de los miembros estructurales (es decir, parámetros de ingeniería). Su uso es, por lo tanto, altamente recomendado, ya que garantiza una estimación precisa de la respuesta no lineal de las estructuras.
- Se invita asimismo a los usuarios a leer el NEHRP Seismic Design Technical Brief No. 4, en el cual el tema del modelado no lineal es ampliamente cubierto.