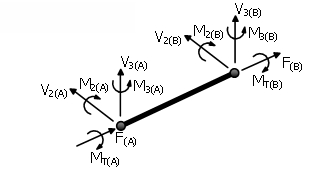
Elemento elástico de pórtico - elfrm

Existen casos en los cuales el uso de un elemento de pórtico (viga, columna) inelástico no es necesario (por ej., análisis de eigenvalores, estructuras sometidas a bajos niveles de excitación y, por lo tanto, que responden dentro de su rango elástico, respuesta dinámica del tablero de un puente, etc.). Para estos casos, puede ser preferible la utilización de elementos de pórtico elásticos lineales, por cuya razón el elemento tipo elfrm ha sido desarrollado e implementado en SeismoStruct.

Con el fin de caracterizar completamente este tipo de elemento, se solicita a los usuarios especificar ya sea una sección ya creada (para la cual el programa calculará automáticamente todas las propiedades mecánicas elásticas necesarias) o los valores personalizados de EA, EI2, EI3 y GJ, donde E es el módulo de elasticidad, A es el área de la sección transversal e I2 e I3 son los momentos de inercia alrededor de los ejes locales (2) y (3). 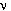La constante torsional es representada mediante J (que no debe ser confundida con el momento de inercia polar), mientras que G representa el módulo de elasticidad transversal, calculado como G=E/(2(1+ )), donde es el coeficiente de Poisson [por ej., ver Pilkey, 1994].

La matriz de rigidez del elemento elfrm, definida en el sistema local, es:

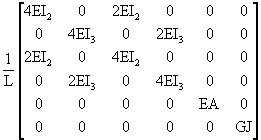
En la ventana de diálogo de este tipo de elemento es también posible definir un valor de amortiguamiento específico del elemento, en oposición al amortiguamiento global definido aquí. Para hacerlo, los usuarios deben simplemente hacer clic sobre el botón Amortiguamiento y seleccionar el tipo de amortiguamiento que mejor represente al elemento en cuestión (por mayores detalles respecto a los tipos de amortiguamiento disponibles y consejos respecto de cuáles pueden ser las mejores opciones, ver el menú Amortiguamiento). Se recuerda asimismo a los usuarios que el amortiguamiento definido a nivel de los elementos prevalece por sobre el amortiguamiento global, es decir, los coeficientes de la matriz de amortiguamiento calculados "a nivel global" asociados a los grados de libertad de un elemento dado serán reemplazados por los coeficientes calculados a través del producto de la matriz de masa del elemento y un parámetro proporcional a la masa, o a través del producto de la matriz de rigidez del elemento y un parámetro proporcional a la rigidez, o mediante el cálculo de una matriz de amortiguamiento de Rayleigh del elemento.

Notas

1. En el elemento elfrm, los efectos de segundo orden (P-delta) así como también los efectos de grandes desplazamientos/rotaciones son debidamente tenidos en cuenta. Sin embargo, los efectos de no linealidad geométrica de las vigas-columna (es decir, el acoplamiento de la rigidez axial y flexional) no son tenidos en cuenta, al menos por el momento.
2. Si se define amortiguamiento de Rayleigh a nivel del elemento utilizando coeficientes diferentes para distintos elementos o respecto de aquellos empleados en los ajustes de amortiguamiento global, entonces se está modelando un amortiguamiento deRayleigh "no-clásico", ya que el amortiguamiento de Rayleigh "clásico" requiere la definición de coeficientes uniformes.

Ejes Locales y Notación del Output