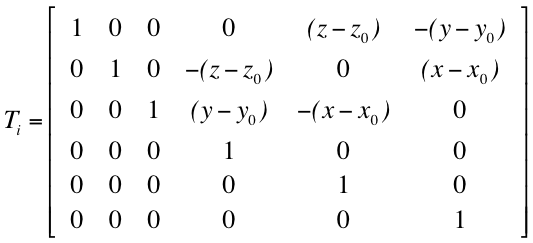Cantidades Modales/de Masa

Este módulo es hace visible solo cuando se llevan a cabo análisis de Eigenvalores o Pushover Adaptativo. El módulo Cantidades Modales/de Masa provee un resumen de (i) los principales resultados modales (es decir, el período/frecuencia natural de vibración de cada modo, los factores de participación modal y las masas modales efectivas), y de (ii) las masas nodales. Estos resultados pueden ser copiados fácilmente a un editor de texto, mediante el menú emergente que aparece al hacer clic derecho con el mouse.

Con respecto a las masas nodales, SeismoStruct provee una tabla en la cual se resumen las masas de los nodos para cada grado de libertad (incluso rotacionales). Para cada nodo, la masa rotacional es calculada como la suma entre la masa rotacional definida específicamente por el usuario para ese nodo y el producto de la masa traslacional del nodo por el cuadrado de la distancia al centro de gravedad del modelo.

Los factores de participación modal, obtenidos como la razón entre el factor de excitación modal () y la masa generalizada (), proveen una medida de cuán fuertemente participa un modo dado en la respuesta dinámica de una estructura. Sin embargo, dado que las formas modales Fn pueden ser normalizadas en formas diferentes, la magnitud absoluta del factor de participación modal no tiene significado alguno y es, en cambio, su magnitud relativa respecto de los restantes modos que resulta de importancia [Priestley et al., 1996].

Por este motivo, y en particular para el caso de los edificios sometidos a un input sísmico, es habitual que los ingenieros/analistas utilicen la masa modal efectiva () como medida de la importancia relativa que cada uno de los modos de la estructura tiene sobre su respuesta dinámica. De hecho, dado que meff,n puede interpretarse como la parte de la masa total M de la estructura que es excitada por un modo n dado, los modos que presenten valores altos de masa modal efectiva son propensos a contribuir significativamente en la respuesta, y viceversa.

Notas

1. Por mayor información respecto del análisis modal y sus respectivos parámetros, se recomienda a los usuarios consultar la literatura disponible [por ej., Clough and Penzien, 1993; Chopra, 1995]
2. Las formas modales se encuentran normalizadas respecto de la masa de manera que Φn=1.
3. Los Factores de Participación Modal (FPMs) para las rotaciones son calculados considerando una matriz de transformación definida de la siguiente manera (donde x0, y0, z0 son las coordenadas del centro de masa), de forma tal que el factor de excitación modal se convierte en 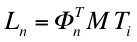, a partir del cual la masa efectiva modal puede ser fácilmente obtenida (como para los grados de libertad traslacionales).