Soil-structure interaction curve - ssi_py
This is a nonlinear dynamic soil-structure interaction (SSI) model, developed and implemented by Allotey and El Naggar [2005a; 2005b], adequate for analysing footings, retaining walls and piles under different loading regimes (the nomenclature chosen for this curve puts in evidence the fact that this model can be used to carry out lateral pile analyses, where p-y curves are commonly employed). It accounts for gap formation with the option of considering soil cave-in, it features cyclic hardening/degradation under variable-amplitude loading, and it can model responses that are bounded or unbounded within their initial backbone curves. Cyclic degradation/hardening due to pore pressure and volumetric changes is accounted for through the use of elliptical damage functions implemented within the framework of a modified rainflow counting algorithm [Anthes, 1997]; the equivalent number of cycles approach [e.g. Seed et al. 1975; Annaki and Lee, 1977] is also used. The effect of soil cave-in is, on the other hand, modelled using an empirically developed hyperbolic function.
Evidently, this hysteretic model, on its own, is not sufficient to model a given foundation system. Instead, a series of springs (i.e. link elements) featuring an appropriately calibrated ssi_py curve must be used, normally in association with a beam-column element, in order to model whatever foundation system the user needs to represent. In other words, this response curve is to be employed within the realms of beam-on-a-nonlinear Winkler foundation (BNWF) model, whereby a number of spring elements are used under the foundation and the response curves have to be given for each. For a footing, the parameters are the same for all springs, whilst for a pile or retaining wall, since the overburden increases with depth, the parameters change with depth.
In addition, and as noted here, viscous damping may be assigned to the link element whenever the user wishes to somehow account for radiation damping effects (this will be similar to the introduction of a dashpt element parallel to the soil spring). Users may refer to the literature [e.g. Wolf, 1994; Allotey and El Naggar, 2005b] for indications on how to compute appropriate values of damping, as a function of the vibration characteristics of the soil-structure system. Commonly, if the vibration period of the soil-structure system is below that of the site, then the effects of radiation damping may be considered as negligible.
Nineteen parameters need to be defined in order to fully characterise this response curve:
1st and 2nd segments of backbone curve (K0, Fc, Fy, 
)
The model idealizes the soil normal force-displacement relations into multi-linear curves. The first segment of the backbone curve has an initial stiffness K0. The second segment of the curve starts at a force Fc (defined as a ratio to Fy), with the stiffness reduced to 
. The second segment ends at the soil yielding strength Fy. The input parameters range as 0 
Fc < 1, and 0.001 1. By default, Fc = 0.5, = 1, and the input of Fc 
1 or 1 results in resetting Fc and to their default values.
3rd and 4th segments — ultimate curve (
and 
)
The stiffness ratio parameter (which defines the stiffness of the 3rd segment in proportion to K0) and the strength ratio parameter (which defines the ultimate strength in proportion to Fy) determine the ultimate behaviour of the backbone. The slope of the third segment can be either positive or negative (i.e. hardening or softening behaviour). The positive slope cannot be greater than the soil second slope, i.e., < is a requirement (it is checked in the program as 0.9). For < 0, the absolute value of the slope cannot be greater than the initial slope, i.e. 
.
The second portion of the ultimate curve always has a zero slope. The strength at the turning point between the third and fourth portions can be specified by the parameter (0). Specifically, < 1 for < 0, = 1 for = 0, and > 1 for > 0. By default, = 1 with = 0, and the ultimate curve represents a one portion horizontal line. The input of > 0 and 1 or vice-versa results in both parameters being reset to the default values.
In the case of an ultimate curve with negative slope (< 0), the response is always set to be bounded within the initial backbone curve; i.e. the flag "/b" is set to be on, regardless of user definition.
Initial Force (P0) and Minimum Force (Pa)
The initial force ratio P0 and the minimum force ratio Pa are designed to represent the initial force present before cycling begins, and a minimum (active) force experienced under negative displacement. They are defined in proportion to Fy. P0 ranges between 0 P0 0.9. P0 > 0 shifts the backbone to the tension side (leftwards), and specifies an initial force at zero displacement. The minimum force Pa is treated as a baseline in the model, and movement never goes below this level. The following conditions apply to Pa: 0 Pa P0 ; Pa Fy ; Pa Fc.
Side Shear Contribution Ratio (fs)
This specifies the inclusion of a side-shear force, which is defined as a ratio of sdFc (see parameters ps and es below). This value is taken into account only when flag "/s" is on, in which case side-shear is assumed to be present and fs is considered instead of Pa (i.e. Pa=0 and the displacement axis is the baseline). The limits of fs are 0 fs 0.9.
Unloading Stiffness Parameter (
)
Depending on flag "/a", may represent a limit to the unload stiffness degradation/hardening factor (flag "/a" off) or specify instead a constant unloading stiffness multiplier (flag "/a" on). When the flag is on, ranges as > 0; a value of > 1 may be used to set the unload stiffness larger than the initial stiffness of the initial backbone curve (the default value however equals 1).
As stated above, when the flag is off, is used as a limiting value of the cyclic unloading stiffness factor ku (see parameters pk and ek below); for degradation (pk<1), pk 1, whilst for hardening (pk>1), 1 pk.
Most experiments do not typically show values of much lower than one, though this is allowed in the model. It is also important to note that the value of affects the computed response in a significant manner, for which reason care should be exercised in its selection; an unrealistic estimate of may lead to very erroneous results.
Stiffness/Strength Degradation/Hardening Parameters (pk, ek, ps, es)
The stiffness (pk, ek) and strength (ps, es) parameters are used to estimate the amount of stiffness and strength degradation/hardening that occurs due to cycling. These are then used in a stress-independent form of the "elliptic" degradation/hardening equation given by Allotey and El Naggar [2005a; 2005b] to compute the stiffness and strength degradation/hardening factors; ku, sd. The values ranges for these parameters are: pk>0, ek>0 and ps>0, es>0; degradations is obtained when pk or ps are lower than 1, otherwise hardening is enforced. For most practical applications, degradation or hardening occur simultaneously for both stiffness and strength (i.e. it is uncommon for strength degradation to occur concurrently to stiffness hardening, or vice-versa); this is however not enforced.
The factors ku and sd are computed on a half-cycle basis, and are therefore evaluated at the beginning of each unload or reload. These values are then applied to the original backbone curve to obtain either the current standard reload curve, or the general unload curve. The following limitations, some of which have already been noted, apply as limiting conditions to the values of these two factors:
- for unloading, only stiffness degradation/hardening is accounted for, and for all cases sd=1
- for unloading, when flag "/a" is on, cyclic stiffness degradation/hardening does not occur, and a constant stiffness factor is assumed, i.e. ku =
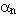
- for unloading, when flag "/a" is off, then 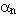represents a maximum/minimum degradation/hardening value, i.e. if pk<1 then ku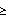 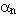, whilst if pk>1 then ku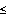
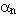
Note: By default, all these parameters are assigned the value of 1, effectively meaning that no degradation/hardening occurs.
S-N Curve Parameters (ks, f0)
The S-N curve describes the cyclic stress ratio (i.e. ratio between the cyclic stress and the initial mean effective stress 
) versus the number of loading cycles, similar to that used in fatigue analysis. It is used to evaluate the incremental damage due to each half-cycle of loading, in order to estimate the cumulative cyclic degradation/hardening at the beginning of each unload or reload. In the model, the S-N curve is expressed as Sr = S/S1 versus the number of cycles, where S and S1 are the stress ratios for the current and first cycles, respectively. Two different forms of the S-N curve are at the user's disposal; if flag "/logS" is on, then a log-log relation is employed, whilst if the flag "/logS" is off, then a semi-log relation is considered instead. The parameter ks is the slope of S-N curve; for the log-log relation, ks is equal to the slope of the conventional S-N curve (ksc), whilst for the semi-log case, ks = ksc/S1 [see Allotey and El Naggar, 2005a; 2005b].
The parameter f0 is the soil stress corresponding to S1, i.e. f0 = S1 (note that the units of must be consistent with those of Fy). The parameter ranges as f0>0, with a default value f0=2Fy, and may be adjusted to account for mean cyclic stress effects [e.g. Hyodo et al., 1994].
Soil Gapping Parameters (p1, p2)
The gap force parameter, p1, is used to estimate the direct reload point (fmm) to which the direct reload curve (DRC) is directed. The value of the parameter ranges between 0 p1 1, with the DRC being parallel to the displacement axis when p1=0, as previously discussed. For reload after movement along the baseline for the case when the flag "/s" is on, this results in the formation of a pure gap. The change from the direct reload curve (DRC) to the standard reload curve (SRC) takes place at the intersection of the DRC and the current baseline standard reload curve (B_SRC). Users are referred to the work of [see Allotey and El Naggar, 2005a; 2005b] for further details. The default value is p1=0, that is, fully-unconfined behaviour is assumed (this would represent, for instance, a full gapping stiff clay-pile response).
The parameter p2 represents the effect of "soil cave-in", and is used to estimate the starting displacement, ds, of the current B_SRC. The parameter ranges as 0 p2, with p2=0 meaning that no soil fall-in takes place (i.e. the B_SRC starts from the current baseline unload displacement point); this is the default assumption.
Flag settings combination
As described above, this response curve makes use of five flags (/logS, /s, /b, /kbu, /a) which can be used to activate or de-activate an equal number of features in the model, also described above. One of two mutually exclusive states (turned on (o) or turned off (x)) might be assigned to each of the five flags, hence it results evident that a total number of 2^5=32 possible flag settings combinations are made available to the user, as shown in the table below. By default, combination no. 31 is employed, meaning that all flags are turned on, that is, (i) a log-log S-N curve is considered, (ii) side-shear is included, (iii) response is bounded, (iv) unload stiffness follows backbone curve, (v) cyclic stiffness degradation/hardening does not occur.
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
21
|
22
|
23
|
24
|
25
|
26
|
27
|
28
|
29
|
30
|
31
|
|
| /logS |
x
|
x
|
x
|
x
|
x
|
x
|
x
|
x
|
x
|
x
|
x
|
x
|
x
|
x
|
x
|
x
|
o
|
o
|
o
|
o
|
o
|
o
|
o
|
o
|
o
|
o
|
o
|
o
|
o
|
o
|
o
|
o
|
| /s |
x
|
x
|
x
|
x
|
x
|
x
|
x
|
x
|
o
|
o
|
o
|
o
|
o
|
o
|
o
|
o
|
x
|
x
|
x
|
x
|
x
|
x
|
x
|
x
|
o
|
o
|
o
|
o
|
o
|
o
|
o
|
o
|
| /b |
x
|
x
|
x
|
x
|
o
|
o
|
o
|
o
|
x
|
x
|
x
|
x
|
o
|
o
|
o
|
o
|
x
|
x
|
x
|
x
|
o
|
o
|
o
|
o
|
x
|
x
|
x
|
x
|
o
|
o
|
o
|
o
|
| /kbu |
x
|
x
|
o
|
o
|
x
|
x
|
o
|
o
|
x
|
x
|
o
|
o
|
x
|
x
|
o
|
o
|
x
|
x
|
o
|
o
|
x
|
x
|
o
|
o
|
x
|
x
|
o
|
o
|
x
|
x
|
o
|
o
|
| /a |
x
|
0
|
x
|
o
|
x
|
o
|
x
|
o
|
x
|
o
|
x
|
o
|
x
|
o
|
x
|
o
|
x
|
o
|
x
|
o
|
x
|
o
|
x
|
o
|
x
|
o
|
x
|
o
|
x
|
o
|
x
|
o
|
Notes
- This versatile hysteretic model is still being tested and further developed. For instance, currently this ssi_py curve caters for the normal force-displacement direction only (i.e. it does not account for the tangential force-slip response). In addition, or perhaps in tandem, the DOFs are not fully coupled (a limitation that is also a consequence of the currently uncoupled nature of the link elements in SeismoStruct). It is envisaged that both of these issues will be addressed in future releases of SeismoStruct.
- Future releases of SeismoStruct are also likely to introduce a significantly more user-friendly way of calibrating/adjusting the parameters of this response curve, using drop-down menus and/or radio buttons to select the different modelling options.
- In recent years, an alternative approach to the modelling of foundation systems, consisting in the employment of a fully-coupled V-H-M (vertical-horizontal-rotation) macro-model has been proposed [e.g. Cremer at al, 2002]. It uses just one element to model the whole footing response and is based on a plasticity-type yield surface formulation. Although this is certainly a promising approach to SSI modelling, it is felt that, given the current state of development and practice, the more traditional BNWF procedure, currently implemented in SeismoStruct through the employment of the powerful ssi_py response curve, provides users with all the facilities required for an adequate modelling of the static, and above all dynamic, interaction between soils, foundations and structures.