Masonry infill strut curve - inf_strut

This is the masonry infill strut model, developed and initially programmed by Crisafulli [1997] and implemented in SeismoStruct by Blandon [2005], to be used (almost exclusively) in association with the infill panel element. Seventeen parameters need to be defined in order to fully characterise this response curve:

Initial Young modulus - Em
The elastic modulus represents the initial slope of the strain-stress curve and its value exhibits a large variation. Since masonry is a composite material consisting of bricks and mortar, each of which feature distinct properties, several researchers [e.g. Ameny et al., 1983; Binda et al., 1988; Drysdale et al., 1994; Sahlin, 1971] assumed linear elastic behaviour for both materials and then that the sum of deformation of the bricks and mortar joints is equal to the compressive deformation of masonry. Other researchers [e.g. Sahlin, 1971; Sinha and Pedreschi, 1983; Hendry, 1990; San Bartolome, 1990; Paulay and Priestley, 1992] considered instead that the modulus of elasticity of the masonry panels could be somehow related to the compressive strength of the material (), defined below. These empirical equations lead typically to values in the following range: 400<Em<1000, as summarised in Crisafulli [1997] and Smyrou [2006]. The upper bound value of 1000 has been proposed by two independent studies [Sahlin, 1971; Paulay and Priestley, 1992] and thus tends to be adopted with some frequency. The range of values for this parameter is extremely wide, herein a default value of 1.6 GPa has been assumed.

Compressive strength -
This compressive strength refers to the diagonal capacity of the infill panel (it does not represent the standard compressive strength of the masonry). If the user does not have access to experimental information on this parameter, then the most correct approach is to calculate a strength value associated to each possible failure mechanism and assign the lowest value obtained to the equivalent diagonal strut, considering it as the resistance corresponding to the most probable mechanism for the infill panel. Bertoldi et al. [1993] have identified four different failure mechanisms and for each of them have developed the following equations:

• Diagonal tension:
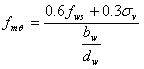
• Sliding shear:
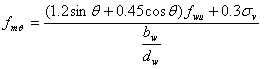
• Compression of corners:
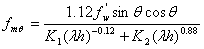
• Compression at center of panel:

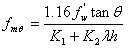
where fws is the shear resistance under diagonal compression, is the vertical compression stress due to gravity loads (typically zero, since infill panels are typically not load-bearing), fwu is the sliding resistance of the mortar joints, f'w is the fundamental compression resistance, is defined in here, h is the interstorey height and the parameters K1 and K2 are expressed as a function of , as shown below.

• if < 3.14, then K1 = 1.3 and K2 = -0.178
• if 3.14 << 7.85, then K1 = 0.707 and K2 = 0.01
• if > 7.85, then K1 = 0.47 and K2 = 0.04

Note: fws, fwu and f'w are obtained from tests on masonry samples.

The range of values for the compressive strength is estremely wide, herein a default value of 1 MPa has been assumed.

Tensile strength - ft
The tensile strength represents the tensile strength of the masonry or the bond-strength of the interface between frame and infill panel. Its presence offers generality in the model but it can even be assumed as equal to zero (default value) since it is much smaller than the compressive strength and will have a relatively minor effect on the overall response. Varum [2003] reported a value of 0.575 MPa, obtained within a diagonal compression tests campaign.

Strain at maximum stress -
This parameter represents the strain at maximum stress and influences, via the modification of the secant stiffness, the ascending branch of the stress-strain curve. This parameter may vary from 0.001 to 0.005, and should be calibrated through the consideration of experimental data. Herein a default value of 0.0012 mm/mm is used.

Ultimate strain -
This strain is used to control the descending branch of the stress-strain curve, modelled with a parabola so as to obtain better control of the strut's response [Crisafulli, 1997]; e.g. for relative large values (such as), the decrease of the compressive strength becomes smoother and the analyses more stable. The default value is 0.024 mm/mm.

Closing strain -
This parameter defines the strain after which the cracks partially close allowing compression stresses to develop. Its value may vary from between 0 and 0.003, as suggested by [Crisafulli, 1997]. Herein, a default value of 0.004 mm/mm has been adopted.

Strut area reduction strain and Residual strut area strain -and
These are the two strains associated to the reduction of the strut area described in here. These are parameters for which it is obviously difficult to find experimental supporting evidence, given the empirical nature of this strut area reduction scheme. Reasonable values of may be in the range of 0.0003 to 0.0008 whilst for values in between 0.0006 and 0.016 may be perhaps considered. The default values adopted herein are 0.0006 for the strut area reduction strain and 0.001 for the residual strut area strain.

Empirical parameters
The masonry infill strut model requires nine empirical curve calibrating factors to be defined, as proposed by Crisafulli [1997]. These are all related to cyclic loading and, as such, will have little influence when a user is running static monotonic analysis (in other words, users running pushover analysis need not to worry about these factors). In addition, sensitivity studies carried out by Smyrou et al. [2006] have also shown that even on those cases where one is running cyclic/dynamic analyses, only three (, , ) of the parameters listed below play a significant role in the quantification of the energy dissipation capacity of the infill panel (i.e. the remaining six parameters are likely not to require any change from the user).

• starting unloading stiffness factor (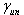), used to define, as a proportion of its loading counterpart, the starting unloading stiffness modulus. Its value may typically vary between 1.5 and 2.5 (though any value above unity constitutes a valid entry), the adopted default being 1.5.
• strain reloading factor (), employed to predict the strain at which the loop reaches the envelope after unloading. Its typical value ranges from 0.2 and 0.4 (though any value above zero constitutes a valid entry), with a default value of 0.2 being adopted here.
• strain inflection factor (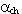), utilised in the computation of the strain at which the reloading curve should feature an inflection point, effectively controlling, in this way, the loops’ fatness. Its value may be found within the interval of 0.1 to 0.7, the latter constituting the default value proposed by SeismoStruct, thus ensuring the highest possible energy dissipation capacity.
• complete unloading strain factor (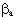), used in the definition of the plastic deformation after complete unloading. Its values typically range between 1.5 and 2.0 (though any value above zero constitutes a valid entry), the former being here adopted as default value.
• stress inflection factor (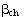), employed in the computation of the stress at which the reloading curve should feature an inflection point. Its value may be found within the interval of 0.5 to 0.9, the latter constituting the default value proposed by SeismoStruct.
• zero stress stiffness factor (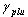), utilised to define, as a proportion of its initial counterpart (Em), the stiffness at zero stress, after complete unloading has taken place. Its value may be found within the interval of 0 to 1, the latter constituting the default value proposed by SeismoStruct.
• reloading stiffness factor (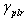), used to define, as a proportion of its loading counterpart, the reloading stiffness modulus, after complete loading has taken place. Its value may typically vary between 1.1 and 1.5 (though any value above unity constitutes a valid entry), the adopted default being 1.5.
• plastic unloading stiffness factor (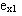), employed to define, as a proportion of its loading counterpart, the unloading tangent modulus corresponding to the plastic strain. Values ranging from 1.5 and 3.0 have been used (though any value above zero constitutes a valid entry), the latter being also the default in SeismoStruct.
• repeated cycle strain factor (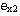), utilised in the computation of the strain that the envelope curve should reach after inner cycling. Its value may typically vary between 1.0 and 1.5 (though any value above zero constitutes a valid entry), the adopted default being 1.4.