Ανελαστικό στοιχείο τοιχοπλήρωσης - infill

Ένα στοιχείο πλήρωσης τοιχοποιίας με τέσσερις κόμβους, που αναπτύχθηκε και αρχικά προγραμματίστηκε από τον Crisafulli [1997] και εφαρμόστηκε στο SeismoStruct από τον Blandon [2005], για την προσομοίωση της μη γραμμικής απόκρισης των στοιχείων πλήρωσης σε πλαισιακές κατασκευές. Κάθε πάνελ αναπαρίσταται από 6 μέλη θλιπτήρων, κάθε διαγώνια κατεύθυνση έχει δύο παράλληλους θλιπτήρες για τη μεταφορά αξονικών φορτίων μεταξύ των δύο απέναντι διαγώνιων γωνιών και έναν τρίτο για τη μεταφορά της τέμνουσας από το άνω στο κάτω μέρος του πάνελ. Αυτός ο τελευταίος θλιπτήρας ενεργεί μόνο κατά τη διαγώνιο που είναι σε θλίψη, γι΄αυτό η ‘ενεργοποίησή’ του εξαρτάται από την παραμόρφωση του πάνελ. Οι θλιπτήρες αξονικού φορτίου χρησιμοποιούν το μοντέλο υστέρησης του θλιπτήρα τοιχοποιίας, ενώ ο θλιπτήρας τέμνουσας χρησιμοποιεί ένα διγραμμικό κανόνα υστέρησης.

Επίσης, όπως μπορεί να παρατηρηθεί στην εικόνα παρακάτω, τέσσερις εσωτερικοί κόμβοι χρησιμοποιούνται για να ληφθούν υπόψη τα πραγματικά σημεία επαφής μεταξύ των πλαισίων και των πάνελ τοιχοπλήρωσης (δηλ. για να λάβουν υπόψη το πλάτος και το ύψος των υποστυλωμάτων και των δοκών αντίστοιχα), ενώ τέσσερις κόμβοι εισάγονται με στόχο να λάβουν υπόψη το μήκος επαφής μεταξύ των πλαισίων και των πάνελ τοιχοπλήρωσης. Όλες οι εσωτερικές δυνάμεις μετατρέπονται στους εξωτερικούς τέσσερις κόμβους (οι οποίοι όπως σημειώνεται εδώ, πρέπει να οριστούν σε αντί-ωρολογιακή σειρά) όπου το στοιχείο συνδέεται στο πλαίσιο.

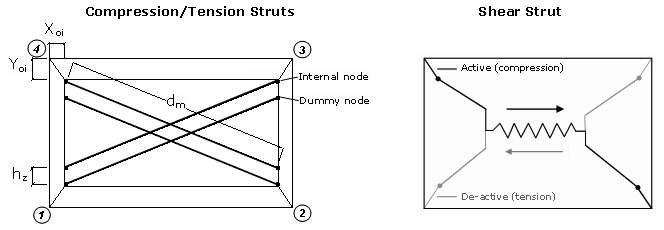
Σημείωση: Παρόλο που τα ανελαστικά στοιχεία τοίχων πλήρωσης έχουν δημιουργηθεί για την προσομοίωση της μη γραμμικής απόκρισης των στοιχείων τοιχοπλήρωσης σε πλαισιακές κατασκευές (όπως αναφέρθηκε παραπάνω), μπορούν επίσης να χρησιμοποιηθούν για την προσομοίωση πλακών με μια συγκεκριμένη συνεισφορά ακαμψίας και ανελαστική συμπεριφορά, π.χ. τοποθετώντας στρατηγικά αυτά τα στοιχεία και/ή ανελαστικά στοιχεία δικτυώματος με τέτοιο ορισμό ιδιοτήτων που να μιμούνται την επιθυμητή συμπεριφορά (όπως συνίσταται εδώ).

Προκειμένου να χαρακτηριστεί πλήρως αυτός ο τύπος στοιχείου, πρέπει να οριστούν τα ακόλουθα:

Παράμετροι Καμπύλης θλιπτήρα
Χρησιμοποιείται στον ορισμό του μοντέλου υστέρησης θλιπτήρα τοιχοποιίας, το οποίο προσομοιώνεται με την inf_strut καμπύλη απόκρισης.

Παράμετροι Καμπύλης Τέμνουσας
Χρησιμοποιείται στον ορισμό του μοντέλου υστέρησης θλιπτήρα τοιχοποιίας, το οποίο προσομοιώνεται με την inf_shear καμπύλη απόκρισης.

Πάχος τοίχου Πλήρωσης - t
Μπορεί να θεωρηθεί ως ίσο με το πλάτος μόνο των τούβλων του πάνελ (π.χ. 12 cm), ή να συμπεριλάβει επίσης τη συνεισφορά του σοβά (π.χ. 12+2x1.5=15 cm).

Μετακίνηση εκτός επιπέδου αστοχίας
Εισάγεται ως ποσοστό του ύψους του ορόφου. Δείχνει την απενεργοποίηση του στοιχείου, δηλ. όταν το πάνελ, όχι το πλαίσιο, φτάνει σε μια εκτός επιπέδου σχετική μετακίνηση, το πάνελ δεν συνεισφέρει πλέον ούτε στην αντοχή ούτε στη δυσκαμψία της κατασκευής, αφού θεωρείται ότι έχει αστοχήσει με ένα εκτός επιπέδου μηχανισμό αστοχίας. (Σημειώνεται ότι δεν έχει εισαχθεί η απενεργοποίηση με βάση την επιτάχυνση, διότι θα ήταν πολύ ευαίσθητο στις υψηλές συχνότητες και/ή σε ψευδείς ιδιομορφές επιτάχυνσης. Όμως, μια λύση παρόλα αυτά συνίσταται στη σημείωση 5, παρακάτω).

Επιφάνεια Θλιπτήρα 1 - A1
Ορίζεται ως το προϊόν του πάχους του πάνελ και του ισοδύναμου πλάτους του θλιπτήρα ( bw), το οποίο κανονικά ποικίλει μεταξύ 10% και 40% της διαγωνίου του πάνελ πλήρωσης (dm), όπως συμπεραίνεται από πολλούς ερευνητές βάσει δεδομένων πειραμάτων και αναλυτικών αποτελεσμάτων. Εντούτοις, υπάρχουν αρκετές εμπειρικές εκφράσεις, με διάφορους βαθμούς πολυπλοκότητας, που έχουν προταθεί από διαφορετικούς συγγραφείς [e.g. Holmes, 1961; Stafford-Smith, 1962; Stafford-Smith and Carter, 1969; Mainstone and Weeks, 1970; Mainstone, 1971; Liauw and Kwan, 1984; Decanini and Fantin, 1986; Paulay and Priestley, 1992], και στους οποίους ο χρήστης μπορεί να ανατρέξει για καθοδήγηση. Έχουν συνοψιστεί στο έργου του Smyrou [2006], όπου οι πραγματικές προτάσεις των Holmes [1961]  ή Paulay and Priestley [1992] δηλαδή η απλή θεώρηση μιας τιμής bw η οποία είναι αντίστοιχα ίση με το 1/3 ή 1/4 του dm συνίσταται ως μια πιθανή διευκόλυνση και όχι απαραίτητα ως ανακριβή τρόπο εκτίμησης της τιμής αυτής της παραμέτρου.

Επιφάνεια Θλιπτήρα 2 - A2
Εισάγεται ως ποσοστό του Α1, αποσκοπεί στο να λάβει υπόψη το γεγονός ότι λόγω ρηγμάτωσης του πάνελ πλήρωσης, το μήκος επαφής μεταξύ του πλαισίου και του πάνελ μειώνεται όσο η πλευρική και συνεπώς η αξονική μετακίνηση αυξάνεται, επηρεάζοντας έτσι το εμβαδόν του ισοδύναμου θλιπτήρα. Θεωρείται ότι το εμβαδόν μεταβάλλεται γραμμικά συναρτήσει της αξονικής παραμόρφωσης (δείτε την παρακάτω εικόνα), με τους δύο θλιπτήρας μεταξύ των οποίων λαμβάνει χώρα αυτή η μεταβολή να ορίζονται ως παράμετροι εισαγωγής για το μοντέλο υστέρησης του θλιπτήρα τοιχοποιίας.

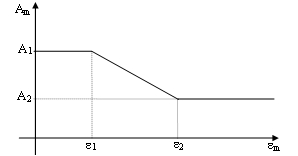
Ισοδύναμο μήκος επαφής  - hz
Εισάγεται ως ποσοστό του κατακόρυφου ύψους των πάνελ, αποδίδοντας αποτελεσματικά στην απόσταση μεταξύ των εσωτερικών (internal) και των «ψεύτικων» (dummy) κόμβων, και χρησιμοποιείται κατά κάποιο τρόπο για να λάβει υπόψη το μήκος επαφής μεταξύ του πλαισίου και του πάνελ πλήρωσης. Λογικά αποτελέσματα προκύπτουν για τιμές 1/3 μέχρι 1/2 του πραγματικού μήκους επαφής  (z), όπως ορίζεται από τον Stafford-Smith [1966]  ως ίσο με 0.5pl^-1, όπου λ είναι μια αδιάστατη παράμετρος σχετικής δυσκαμψίας που υπολογίζεται από την εξίσωση που δίνεται παρακάτω, στην οποία E_m είναι το μέτρο ελαστικότητας της τοιχοποιίας, t_w είναι το πάχος του πάνελ, θ είναι η γωνία του διαγώνιου θλιπτήρα σε σχέση με τις δοκούς, E_cI_c είναι η δυσκαμψία κάμψης των υποστυλωμάτων, και h_w είναι το ύψος του πάνελ πλήρωσης.

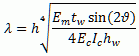
Οριζόντια και Κατακόρυφη μετάθεση - xoi και yoi
Εισάγεται ως ποσοστό των οριζόντιων και κατακόρυφων διαστάσεων του πάνελ, προφανώς αναπαριστούν την μείωση των τελευταίων λόγω του βάθους των πλαισιακών στοιχείων. Με άλλα λόγια, αυτοί οι παράμετροι παρέχουν την απόσταση μεταξύ των εξωτερικών γωνιακών κόμβων και των εσωτερικών.

Ποσοστό δυσκαμψίας που αποδίδεται στην τέμνουσα -
Αναπαριστά το ποσοστό της δυσκαμψίας του πάνελ (υπολογίζεται εσωτερικά από το πρόγραμμα) που πρέπει να οριστεί στο ελατήριο τέμνουσας (τυπικά, μια τιμή μεταξύ 0.2 και 0.6 χρησιμοποιείται). Με άλλα λόγια, η δυσκαμψία του θλιπτήρα (KA) και η δυσκαμψία τέμνουσας (KS) υπολογίζονται ως ακολούθως:

Ειδικό βάρος -
Αναπαριστά το ογκομετρικό βάρος του πάνελ (υπενθυμίζεται ότι σε αυτό το στοιχείο δεν ορίζεται διατομή, εξ’ου δεν ορίζεται υλικό, οπότε το ίδιο βάρος πρέπει να οριστεί εδώ). Η προεπιλεγμένη τιμή είναι 20 kN/m3.

Στο πλαίσιο διαλόγου αυτού του στοιχείου είναι δυνατόν να ορίσετε μια συγκεκριμένη απόσβεση στοιχείου, σε αντίθεση με την καθολική απόσβεση που περιγράφεται εδώ. Προκειμένου να γίνει αυτό οι χρήστες πρέπει απλώς να πατήσουν το κουμπί Απόσβεση και μετά να επιλέξουν τον τύπο απόσβεσης που ταιριάζει καλύτερα στο συγκεκριμένο στοιχείο (οι χρήστες πρέπει να ανατρέξουν στο μενού Απόσβεση για να αποκτήσουν εικόνα των διαθέσιμων διαφορετικών τύπων απόσβεσης και για συμβουλές για το ποιες μπορεί να είναι οι καλύτερες επιλογές). Υπενθυμίζεται επίσης στους χρήστες ότι η απόσβεση που ορίζεται σε επίπεδο στοιχείου, έχει προβάδισμα έναντι της καθολικής απόσβεσης, που σημαίνει ότι οι ‘καθολικά-υπολογισμένοι’ συντελεστές του μητρώου απόσβεσης που σχετίζονται με τους βαθμούς ελευθερίας ενός δεδομένου στοιχείου, θα αντικατασταθούν από συντελεστές που θα έχουν υπολογιστεί μέσω πολλαπλασιασμού του μητρώου μάζας του στοιχείου με μια παράμετρο ανάλογη της μάζας, ή μέσω του υπολογισμού του μητρώου απόσβεσης Rayleigh του στοιχείου.

Σημειώσεις

1. Αυτό το μοντέλο (με τη διάταξη των θλιπτήρων του) είναι ικανό να περιγράψει μόνο τους πιο κοινούς τρόπους αστοχίας, αφού ένα μοντέλο που θα λάμβανε υπόψη όλους τους τύπους αστοχίας τοιχοποιίας δεν θα ήταν πρακτικό λόγω συνθετότητας και μεγάλων αβεβαιοτήτων. Συνίσταται στους χρήστες να συμβουλευτούν τις δημοσιεύσεις των Crisafulli et al. [2000] και Smyrou et al. [2006] για περισσότερες λεπτομέρειες πάνω σε αυτό το μοντέλο.
2. Η αντοχή και η δυσκαμψία των τοίχων πλήρωσης εισάγονται μετά την εφαρμογή των αρχικών φορτίων, ώστε τα πρώτα να μην αντιστέκονται στα φορτία βαρύτητας (τα οποία κανονικά απορροφούνται από τα γειτονικά πλαίσια, που κατασκευάστηκαν πρώτα). Αν οι χρήστες επιθυμούν οι τοίχοι πλήρωσης να παραλάβουν φορτία βαρύτητας, πρέπει να ορίσουν τα τελευταία ως μη αρχικά φορτία. 
3. Σε πολύ «προσεγμένα» μοντέλα, οι χρήστες μπορεί να επιθυμούν να εισάγουν στοιχεία συνδέσμου μεταξύ των πλαισίων και των κόμβων των πάνελ πλήρωσης, προκειμένου να λάβουν υπόψη το γεγονός ότι τα πάνελ δεν είναι πλήρως άκαμπτα συνδεδεμένα με τα γύρω πλαίσια.
4. Οι χρήστες μπορεί επίσης να επιθυμούν να ελέγξουν για τιμές εκτός επιπέδου επιτάχυνσης και να θέσουν ένα όριο η υπέρβαση του οποίου μπορεί να σημαίνει εκτός επιπέδου αστοχία του πάνελ (μετά μπορεί να ρυθμιστεί απενεργοποίηση του στοιχείου στο χρόνο που αντιστοιχεί στην επίτευξη τέτοιων τιμών επιτάχυνσης).
5. Η παρουσία ανοιγμάτων στα πάνελ τοιχοπλήρωσης προσδίδει μια σημαντική αβεβαιότητα στην εκτίμηση της συμπεριφοράς των πλαισίων που έχουν πλήρωση. Πολλοί ερευνητές [ e.g. Benjamin and Williams, 1958; Fiorato et al., 1970; Mallick and Garg, 1971; Liauw and Lee, 1977; Utku, 1980; Dawe and Young, 1985; Thiruvengadam, 1985; Giannakas et al., 1987; Papia, 1988; Dawe and Seah, 1989; Hamburger, 1993; Bertoldi et al., 1994; CEB, 1996; Mosalam et al., 1997; Gostic and Zarnic, 1999; De Sortis et al., 1999; Asteris, 2003] έχουν ερευνήσει την επιρροή που μπορεί να έχουν διαφορετικές διατάξεις ανοιγμάτων (σε όρους μεγέθους και θέσης) στην αντοχή και τη δυσκαμψία. Δυστυχώς όμως, αν και κατανοητό λόγω των πολλών μεταβλητών και μεγάλων αβεβαιοτήτων που περιλαμβάνονται, δεν έχει επιτευχθεί σύγκλιση απόψεων πάνω σε αυτό το θέμα. Οι παραπάνω δημοσιεύσεις έχουν όλες οδηγήσει σε διαφορετικά αριθμητικά συμπεράσματα και διαφορετικές συστάσεις. Επομένως οι χρήστες θα πρέπει να βασιστούν στη δική τους ‘κρίση-μηχανικού’ και εμπειρία, μαζί με μια βαθιά μελέτη της βιβλιογραφίας πάνω σε αυτό το θέμα (ένα μικρό ποσοστό της οποίας αναφέρεται παραπάνω), προκειμένου να αποφασίσουν πως θα ληφθούν υπόψη οι επιδράσεις των ανοιγμάτων στην υπό μελέτη κατασκευή. Ως μια διευκόλυνση μπορεί να υποτεθεί ότι οι επιδράσεις των ανοιγμάτων στην απόκριση του πλαισίου που έχει τοίχο πλήρωσης μπορεί να ληφθεί υπόψη ρεαλιστικά μειώνοντας της τιμής του Εμβαδού των Θλιπτήρων (A1), και έτσι την δυσκαμψία του πάνελ, σε αναλογία με το εμβαδόν του ανοίγματος σε σχέση με το πάνελ. Αυτό, όπως φαίνεται από τον Smyrou et al. [2006], αν ένας δεδομένος τοίχος πλήρωσης έχει ανοίγματα από 15% μέχρι 30% σε σχέση με το εμβαδόν του τοίχου, καλή πρόβλεψη απόκρισης μπορεί να αποκτηθεί με μείωση των τιμών του Α1 (δηλ. της δυσκαμψίας) με μια τιμή που κυμαίνεται μεταξύ 30% και 50%. Εφόσον η αντοχή του πάνελ πρέπει να ληφθεί υπόψη, και δεδομένου της πολυποίκιλης φύσης των παρατηρήσεων πάνω σε αυτό το θέμα από τους ερευνητές στο παρελθόν, θα μπορούσαμε ίσως να προτείνουμε, εν απουσία επαρκών αποδείξεων, οι χρήστες δεν πρέπει να αλλάξουν αυτήν την τιμή για να λάβουν υπόψη την παρουσία τυπικών ανοιγμάτων (δηλ. ανοιγμάτων που δεν είναι μεγαλύτερα από το 30% της εμβαδού του τοίχου πλήρωση.
6. Επίσης συνίσταται στους χρήστες να διαβάσουν τις δημοσιεύσεις των Celarec and Dolšek [2012] στις οποίες ερευνώνται οι επιδράσεις της τοιχοποιίας πλήρωσης στην απαίτηση σε τέμνουσα και στην αστοχία υποστυλωμάτων, στην περίπτωση που προσομοιώνονται πλαίσια οπλισμένου σκυροδέματος με τέτοια πάνελ, ως απλοποιημένα μη γραμμικά μοντέλα που δεν είναι ικανά να προσομοιώσουν άμεσα αυτές τις επιδράσεις.