Macroelemento SSI para Pilas de Cimentación - ssiIlink2
Este elemento extiende la aplicación de macroelementos no lineal para el análisis de pilas flexibles cargadas lateralmente y de la interacción de la estructura con la pila y del suelo. Se basa en el trabajo de Correia y Pecker [2019b]. La respuesta lateral de todo el sistema de la pila y del suelo a las acciones sísmicas se condensa en la parte superior de la pila, representada por un elemento con longitud igual a cero ubicado en la base de las columnas y sujeto al movimiento de la base, como se muestra en la Figura abajo.
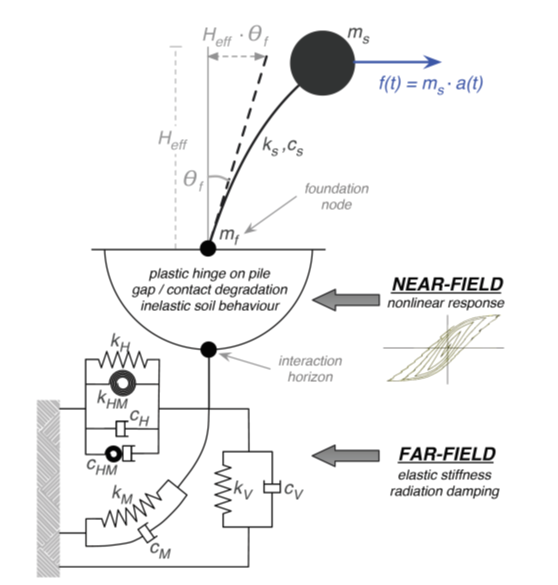
El modelo de macroelemento de la parte superior de la pila representa el comportamiento lateral de las pilas verticales individuales, sometidas a una carga horizontal y un momento, desde las etapas iniciales de carga hasta llegar a la falla. Los efectos de la carga vertical no se consideran directamente en este modelo, excepto por la influencia de la carga vertical en el momento plástico de la sección de la pila. De lo contrario, se considera que la zona superior del perfil del suelo, hasta la profundidad a la que se formará la rótula plástica, solo contribuye a la resistencia de carga lateral. Se supone que la carga vertical se transfiere al suelo circundante por debajo de esa profundidad, donde no hay influencia de la profoundidad de la apertura.
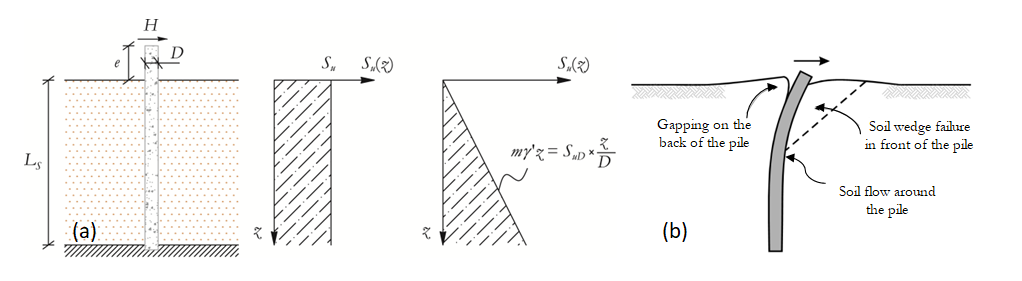
Se considera un depósito de suelo saturado y, ante el movimiento sísmico, se supone que es impermeable. Por lo tanto, se considera que el suelo tiene un comportamiento no drenado ya que el objetivo del macroelemento es simular la respuesta de la pila bajo acciones sísmicas o cargas cíclicas duración corta, y se supone que el criterio de falla de Tresca es válido. La Figura abajo representa los dos escenarios geotécnicos simplificados considerados, en términos de distribución de resistencia al corte (Su) sin drenaje a lo largo de la profundidad del depósito del suelo: constante o lineal. La Figura 2b ilustra la respuesta característica del suelo para una pila larga cargada lateralmente, es decir: una falla en cuña pasiva del suelo a poca profundidad y una falla de tipo “flow around” a profundidades mayores, con una posible formación de apertura en la parte de atrás de la pila.
El macroelemento propuesto se basa en las tres características principales del comportamiento de las pilas cargadas lateralmente, es decir:
i) Respuesta elástica inicial,
ii) apertura y clausura de la abertura,
iii) Condiciones de carga de falla .
El modelo de plasticidad de la superficie delimitadora se utiliza para representar una transición continua entre la respuesta elástica inicial y el flujo plástico en caso de falla, para condiciones de carga monotónica y cíclica de la parte superior de la pila. El comportamiento de la abertura está representado por un modelo elástico no lineal que, sin embargo, tiene en cuenta y está influenciado por el estado de deformación plástica en el suelo circundante.
La superficie delimitadora en el modelo de macroelemento corresponde a la superficie de falla para pilas cargadas lateralmente. Dado que no hay evidencia que demuestre que se debe considerar un comportamiento no asociado, se usa la plasticidad asociada y la superficie límite actúa simultáneamente como la superficie plástica potencial. No se consideran efectos de carga axial en esta formulación de macroelementos y, en consecuencia, la superficie de falla se define en el espacio de carga de la fuerza horizontal y el momento de la parte superior de la pila solamente. Además, se supone una carga plana.
Una superficie de falla aproximada "redondeada" se propuso en Correia y Pecker [2019a], que se basa en el superelipse. Suponiendo un superelipse centrado en el punto de coordenadas (Hc, Mc), con una longitud de eje horizontal y una longitud de eje vertical My, que también se superpone a una distorsión de su forma, γ <0, esta superficie de falla aproximada se puede expresar como:

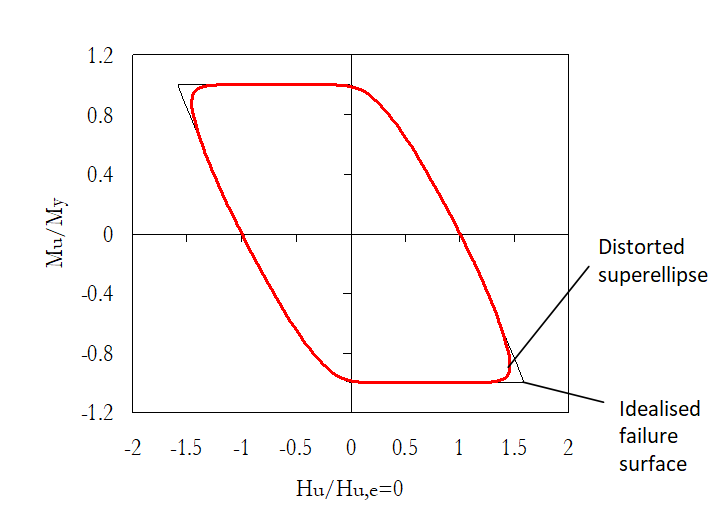
Los exponentes positivos nH y nM controlan la curvatura de los lados del superelipse. La Figura abajo representa la configuración de superrelipse distorsionada, centrada en el origen (Hc = Mc = 0), con sus parámetros calibrados para ajustar la superficie de falla para el perfil de suelo lineal de Su.
Este macroelemento requiere la definición de 23 parámetros de entrada:
El diámetro de la pila (DIAM)
La rigidez de la pila para las direcciones vertical, horizontal y de rotación (K_VV, K_HH, K_MM, K_HM, K_TT)
La capacidad de pila (QQ_H_MAX, QQ_M_MAX)
Los parámetros de la Superellipse BS (Exp_nH,Exp_nM, GAMMA)
La profundidad máxima de la abertura (ZW)
Rigidez a la flexión de la pila (Eplp)
El parámetro de la evolución de la abertura (BETA)
El parámetro de la evolución de la abertura mínimo (ETA)
El parámetro de módulo plástico de referencia (PL_H0)
El exponente para la evolución del módulo plástico (PL_nur)
El valor límite inferior para el Delta en descarga / recarga (Delta_LIM)
La rigidez a la flexión de la pila,(EpIp)eff , se puede calcular fácilmente, mientras que el momento de fluencia de la pila, My, se puede calcular utilizando cualquier herramienta de análisis de sección (y considerando la carga vertical estática en la pila). Por otro lado, las fórmulas para Hu, e = 0 y zw, se derivan por Correia y Pecker [2019a].
Gazetas [1991] proporciona fórmulas para un cálculo directo de la rigidez lateral y axial de la parte superior de la pila y los coeficientes de amortiguación. Estos son válidos para perfiles de suelo con aumento constante, lineal o parabólico de la rigidez del suelo con profundidad, que son representativos de arcilla OC, arcilla NC y arena, respectivamente. La Figura siguente representa la evolución de la rigidez del suelo con profundidad en tales perfiles de suelo idealizados.
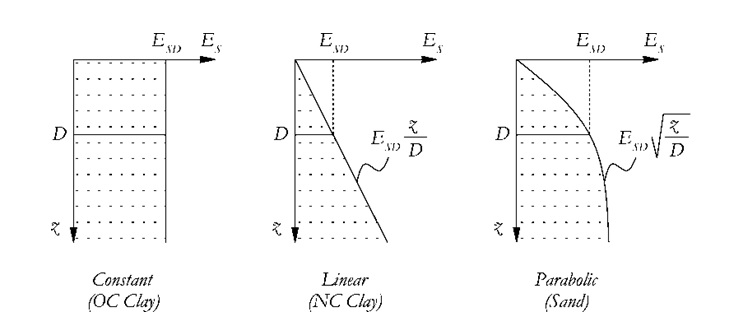
Las expresiones de Gazetas [1991] para las rigideces estáticas de la parte superior de la pila se han adoptado, con pocas modificaciones, en la versión actual de EC 8 - Parte 5 [2003]. Estos son válidos para pilas flexibles o largas y se resumen en la Tabla abajo.
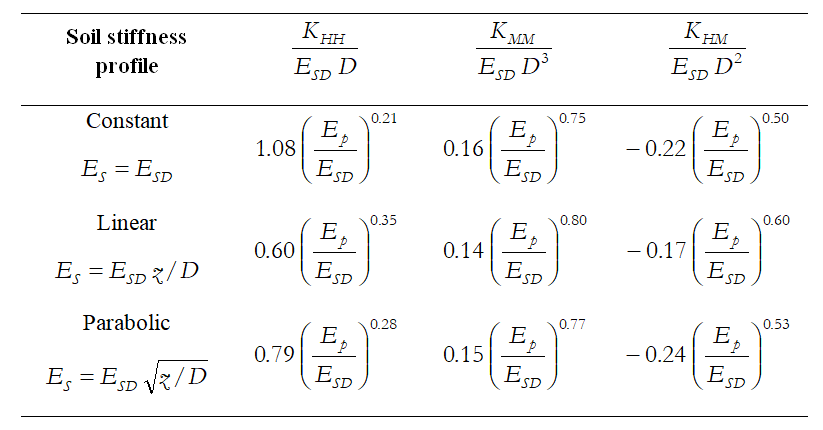
En esas expresiones, D es el diámetro de la pila, ESD es el módulo de deformación del suelo a una profundidad igual al diámetro de la pila y Ep es el módulo de Young del material de la pila. Los componentes de la matriz de rigidez de la parte superior de la pila siguen la convención de signos expresada en la Figura siguente.
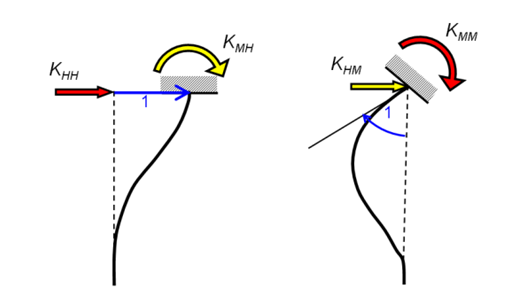
Gazetas [1991] también presenta los correspondientes coeficientes de amortiguamiento de la parte superior de la pila, que se calculan para cada frecuencia f de acuerdo con las expresiones de la Tabla siguente.
Gazetas [1984] ha demostrado que los componentes dinámicos de las rigideces de la parte superior de la pila son aproximadamente iguales a uno, para el rango de frecuencia habitual de interés para la respuesta estructural. Por lo tanto, las rigideces estáticas de la parte superior de la pila se pueden usar aproximadamente como dinámicas, para pilas flexibles individuales. La variación de los componentes de la razón de amortiguamiento con la frecuencia es lineal, según lo predicho por las expresiones en la Tabla siguente. Esto significa que el comportamiento de amortiguamiento de la radiación puede ser aproximado por dashpots con coeficiente de amortiguamiento constante C.

Los parámetros de la superficie delimitadora son fijos para cada uno de los perfiles de resistencia del suelo y se muestran en la Tabla 3. El valor límite δLim es un parámetro relacionado con la convergencia numérica y varía entre 0.01 y 0.2, con un valor predeterminado de 0.1.
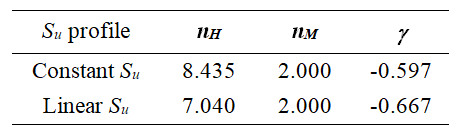
Finalmente, con respecto a los 4 parámetros de calibración restantes, 2 de ellos están relacionados con la respuesta monotónica –ß y H0pl, y los otros 2 están relacionados con el comportamiento cíclico –η y nUR. Alternativamente, 2 de los parámetros están relacionados con el comportamiento de la abertura –ß y η, y los otros 2 están relacionados con el modelo de plasticidad H0pl- y nUR. Los parámetros b y nUR son siempre positivos, mientras que η también puede ser igual a cero si no se considera la profundidad de la abertura residual. Sus valores predeterminados y rangos de variación se presentan en la Tabla siguente.

Contexto teórico sobre el análisis de SSI
El análisis de SSI puede llevarse a cabo mediante el empleo de un modelo de elementos finitos sólidos no lineales (por ejemplo, bloque de suelo), o mediante un contexto de subestructura más simple y, por lo tanto, más práctico, que es el que se puede adoptar en SeismoStruct.
En principio, cuando se modela SSI utilizando el método de subestructura, primero se debe analizar la interacción cinemática con el modelo completo del suelo y la estructura, con la rigidez estructural pero sin masa estructural. En dicho procedimiento, la propagación de la acción sísmica en el suelo se modela explícitamente, típicamente en el dominio de la frecuencia (aunque no necesariamente), y el resultado final es el movimiento del suelo de input (FIM), es decir, el movimiento de la zapata si no tuviera masa. Sin embargo, este paso inicial a menudo se evita asumiendo que la interacción cinemática puede descuidarse y, por lo tanto, utilizando el movimiento del suelo como FIM (este movimiento del suelo también se supone a menudo como resultado de la propagación vertical de las ondas de corte a través de capas del suelo horizontales).
Un paso segundo en el modelado de SSI usando el método de la subestructura sería el cálculo de las impedancias de la zapata (es decir, las propiedades de respuesta dinámica de la zapata), típicamente representadas por un conjunto de resortes, dashpots (y posiblemente masas ficticias para obtener la frecuencia correcta - dependencia de las impedancias). Este segundo paso puede simplificarse determinando las impedancias de las expresiones existentes en la literatura.
El paso final es el análisis de la estructura, con su rigidez y masa, apoyada en las impedancias de los cimientos y sometida a la FIM. Esto es lo que se puede hacer en SeismoStruct, que presenta la ventaja adicional de poder, a través del empleo del macroelemento SSI, considerar también la respuesta no lineal del sistema base. En otras palabras, un análisis SSI llevado a cabo utilizando este macroelemento corresponde a un enfoque híbrido entre el análisis de interacción inercial del enfoque de subestructura, que es estrictamente válido solo para respuesta lineal, y un modelado de elementos finitos sólidos no lineales de efectos SSI .
Por lo tanto, dentro del contexto definido anteriormente, el usuario debe tener en cuenta los siguientes:
A. El método de subestructura solo es teóricamente correcto si la respuesta es lineal, es decir, sin deslizamiento o elevación de una zapata, separación de una pila, degradación de la rigidez, comportamiento plástico y desplazamientos irrecuperables; en presencia de no linealidades, por lo tanto, este tipo de análisis inevitablemente implica cierto grado de aproximación.
B. Como ya se señaló, el FIM es el movimiento sísmico de input que tendría la zapata solo si no tuviera masa (así como el resto de la estructura) y si se comportara linealmente. De hecho, y por ejemplo, si el modelo de una zapata simula su resistencia al deslizamiento, y si hay una masa estructural, el movimiento de la zapata ya no será el FIM debido a las fuerzas de inercia provenientes de arriba y de un posible deslizamiento de la Fundación. Además, incluso en el caso de una respuesta lineal y solo una zapata base con su masa (sin estructura arriba), el movimiento de la zapata no será exactamente el FIM debido a las fuerzas de inercia generadas por la masa de la zapata.
C. La acción sísmica de input para el análisis de SSI utilizando el enfoque de subestructura (como se hace en SeismoStruct) puede consistir en uno de los siguientes:
• historial de aceleración en el nodo base fijo del macroelemento (este debería ser el FIM, a menudo se supone que es equivalente al movimiento de suelo, como ya se discutió), que luego se propagará a través del macroelemento y excitará las masas estructurales (incluida la massa de la zapata);
• Historiales de tiempo de fuerzas de inercia, calculadas como el producto de masas estructurales (incluidas las de la zapata) por la FIM, aplicadas a cada una de las masas de la estructura.
Se supone que estos dos enfoques de definición de input sísmico conducen a resultados de análisis idénticos en términos de desplazamientos relativos nodales (y, por lo tanto, deformaciones / esfuerzos materiales y fuerzas internas de los miembros). El primer enfoque es más fácil de aplicar porque solo se necesita definir un movimiento de base en los nodos fijos. Sin embargo, pueden aparecer problemas numéricos en casos especiales cuando las rigideces del macroelemento son muy grandes. El segundo enfoque es más difícil de aplicar, ya que uno tiene que aplicar un historial de tiempo de fuerza dinámica en todos los nodos con masas agrupadas y se vuelve engorroso cuando se usan masas distribuidas. Pero este método funciona en todos los casos.
Notas
1. Se debe tener cuidado con el movimiento de tierra de entrada cuando se realiza un análisis dinámico ‘time-hostory’ con el macroelemento SSI. De hecho, dado que los dos nodos del macroelemento deben tener el mismo movimiento sin interacción inercial está presente, la forma mejor de realizar el análisis es imponiendo las fuerzas de inercia correspondientes en las masas estructurales de arriba y no imponiendo la historia de aceleración del movimiento del suelo en el nodo base.
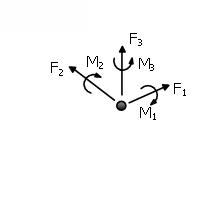
Ejes Locales y Notación del Output