Macroelemento SSI para Cimentaciones Superficiales - ssiIlink1

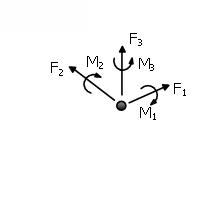
Este elemento es un modelo de macroelementos no lineal para la interacción entre la estructura  y el suelo para las zapatas superficiales, basado en el trabajo de Correia y Paolucci [2019]. Este enfoque de macroelementos reduce significativamente el tamaño del problema, ya que la base y el suelo se consideran un macroelemento único caracterizado por seis grados de libertad (6 DOF), en el caso 3D, cuya formulación se basa en el fuerzas y desplazamientos resultantes. La geometría considerada aquí corresponde a una zapata rígida rectangular, con acoplamiento entre todos los DOF de macroelementos y su definición como un único elemento de link  de longitud cero. Considerando una carga plana, por simplicidad de notación y visualización, la zapata esta sujeta a un momento de volteo y a las fuerzas verticales y horizontales (My, N y Hx respectivamente), como se muestra en la Figura abajo.

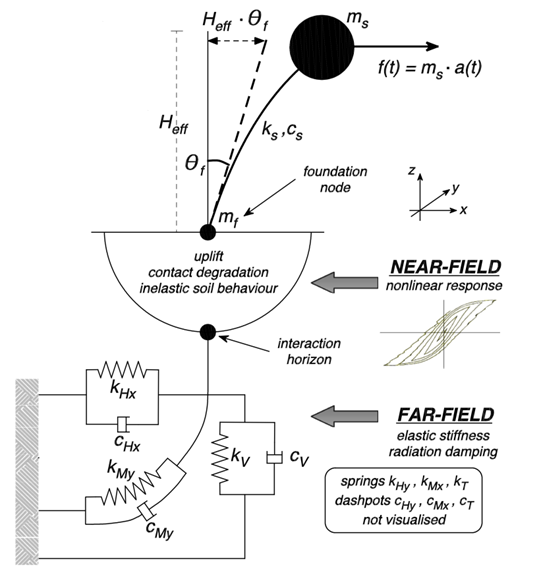
Se adopta un modelo de levantamiento que se basa en una respuesta de levantamiento elástica no lineal que también considera degradación del contacto en la interfaz suelo/zapata debido a cambios irrecuperables en su geometría. También se utiliza un modelo de plasticidad de la superficie delimitadora que tiene en cuenta correctamente la respuestas simultáneas de levantamiento elástico y plástico no lineal. Finalmente, esta formulación de macroelementos es totalmente aplicable a casos de carga tridimensional. La figura abajo representa esquemáticamente el tipo de fenómenos que se pretende modelar con el macroelemento.

El modelo de macroelemento de zapata representa el comportamiento dinámico de zapatas rígidas únicas, sometidas a una carga inercial tridimensional, desde las etapas iniciales de carga hasta llegar a la falla. El macroelemento se basa en las tres características principales de la respuesta de zapatas, a saber:

i)        Respuesta elástica inicial,

ii)      levantamiento en la respuesta de volteo,

iii)    Condiciones de carga de falla.

El modelo de plasticidad de la superficie delimitadora se usa para representar una transición continua entre la respuesta elástica inicial y el flujo de plástico en caso de falla, para condiciones de carga monotónicas, cíclicas y dinámicas. El fenómeno de levantamiento está representado por un modelo elástico no lineal que, sin embargo, tiene en cuenta y está influenciado por el estado de deformación plástica en el suelo subyacente.

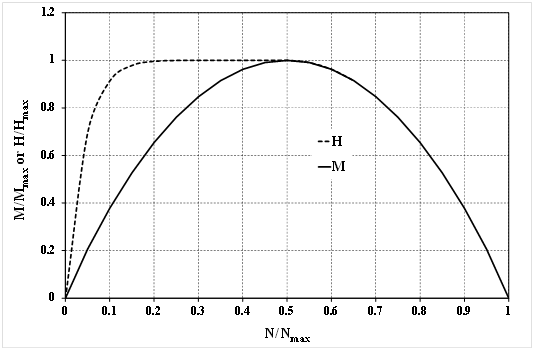
La superficie delimitadora adoptada en este macroelemento depende del tipo de suelo y su condiciones de drenaje durante un evento sísmico. Por lo tanto, se consideran diferentes superficies de falla 3D para condiciones de drenaje y sin drenaje. La superficie final adoptada para describir el comportamiento drenado corresponde a la forma de "pelota de rugby", mientras que para la carga no drenada, la superficie final corresponde a la forma denominada "escalope", que se representa en la Figura 3 en términos de su intersección en los planos de carga H-N y M-N. La forma de "pelota de rugby" corresponde a tener la superficie final representada por la línea continua en ambos planos de carga.

El modelo de macroelemento requiere la definición de 25 parámetros, de los cuales solo 3 deben calibrarse. Los parámetros del modelo junto con su definición y valores sugeridos se dan en la Tabla 1 y corresponden a :

• Las dimensiones de la zapata (longitud, L y ancho, B).

• Seis componentes de rigidez inicial de la zapata, indicados como KN1, KH2, KH3, KM2, KM3, KM2, KTT para direcciones vertical, horizontal y rotacional, respectivamente. Los componentes pueden evaluarse mediante el uso de fórmulas de la literatura (por ejemplo, [Gazetas, 1991]), o calibrarse en resultados de pruebas. Lo mismo se aplica a los seis coeficientes de dashpot equivalentes correspondientes para la representación de amortiguación de radiación.

• la capacidad portante vertical centrada máxima Nmax que corresponde a la capacidad portante estática final de la zapata y puede evaluarse con  fórmulas de superposición estándar (por ejemplo, [Brinch-Hansen, 1970])

• las capacidades máximas de corte de la zapata Hmax2 y Hmax3 y las capacidades máximas de momento la zapata Mmax2, Mmax3, Tmax, que pueden calibrarse en función de las propiedades del material (por ejemplo, ángulo de fricción del suelo) o de valores teoréticas [Butterfield and Gottardi, 1994].

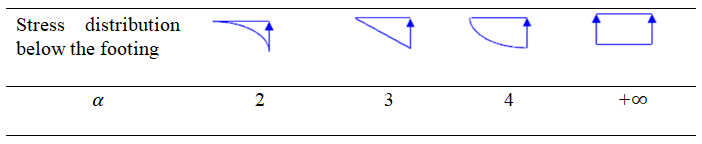
• el parámetro de inicio del levantamiento, α, solo depende de la distribución de los esfuerzos verticales debajo de la zapata y puede determinarse a partir de consideraciones estáticas simples, como se muestra en la Tabla 2. El parámetro no afecta mucho los resultados, y generalmente se toma igual a 3, que corresponde a asumir una distribución lineal de esfuerzos para el suelo al comienzo del análisis.

• el exponente para la historia de carga en descarga/recarga, nUR, suele ser igual a 1, y esta relacionado con diferentes valores de módulo de plástico para descarga/recarga en comparación con la carga virgen

• el parámetro de degradación del contacto entre el suelo y la zapata, dθ, tiene en cuenta la disminución del área de contacto debido al volteo inelástico acumulativo en el modelo de daños y puede evaluarse en función de los resultados experimentales;

• el módulo plástico de referencia normalizado, H0pl que esta calibrado a base de resultados experimentales

• y el parámetro de superficie de potencial plástico, 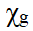, también calibrado a base de resultados experimentales

De lo anterior, resulta que, cuando se conocen los parámetros clásicos de elasticidad y resistencia para el sistema de cimentación y del suelo, queda un pequeño número de 3 parámetros libres para ser calibrados en el proceso de validación, estos parámetros son:  el módulo plástico de referencia normalizado, , el parámetro de superficie de potencial plástico, y , el parámetro del modelo de daño.

Contexto teórico sobre el análisis de SSI

El análisis de SSI puede llevarse a cabo mediante el empleo de un modelo de elementos finitos sólidos no lineales (por ejemplo, bloque de suelo), o mediante un contexto de subestructura más simple y, por lo tanto, más práctico, que es el que se puede adoptar en SeismoStruct.

En principio, cuando se modela SSI utilizando el método de subestructura, primero se debe analizar la interacción cinemática con el modelo completo del suelo y la estructura, con la rigidez estructural pero sin masa estructural. En dicho procedimiento, la propagación de la acción sísmica en el suelo se modela explícitamente, típicamente en el dominio de la frecuencia (aunque no necesariamente), y el resultado final es el movimiento del suelo de input (FIM), es decir, el movimiento de la zapata si no tuviera masa. Sin embargo, este paso inicial a menudo se evita asumiendo que la interacción cinemática puede descuidarse y, por lo tanto, utilizando el movimiento del suelo como FIM (este movimiento del suelo también se supone a menudo como resultado de la propagación vertical de las ondas de corte a través de capas del suelo horizontales).

Un paso segundo en el modelado de SSI usando el método de la subestructura sería el cálculo de las impedancias de la zapata (es decir, las propiedades de respuesta dinámica de la zapata), típicamente representadas por un conjunto de resortes, dashpots (y posiblemente masas ficticias para obtener la frecuencia correcta - dependencia de las impedancias). Este segundo paso puede simplificarse determinando las impedancias de las expresiones existentes en la literatura.

El paso final es el análisis de la estructura, con su rigidez y masa, apoyada en las impedancias de los cimientos y sometida a la FIM. Esto es lo que se puede hacer en SeismoStruct, que presenta la ventaja adicional de poder, a través del empleo del macroelemento SSI, considerar también la respuesta no lineal del sistema base. En otras palabras, un análisis SSI llevado a cabo utilizando este macroelemento corresponde a un enfoque híbrido entre el análisis de interacción inercial del enfoque de subestructura, que es estrictamente válido solo para respuesta lineal, y un modelado de elementos finitos sólidos no lineales de efectos SSI .

Por lo tanto, dentro del contexto definido anteriormente, el usuario debe tener en cuenta los siguientes:

A. El método de subestructura solo es teóricamente correcto si la respuesta es lineal, es decir, sin deslizamiento o elevación de una zapata, separación de una pila, degradación de la rigidez, comportamiento plástico y desplazamientos irrecuperables; en presencia de no linealidades, por lo tanto, este tipo de análisis inevitablemente implica cierto grado de aproximación.

B. Como ya se señaló, el FIM es el movimiento sísmico de input que tendría la zapata solo si no tuviera masa (así como el resto de la estructura) y si se comportara linealmente. De hecho, y por ejemplo, si el modelo de una zapata simula su resistencia al deslizamiento, y si hay una masa estructural, el movimiento de la zapata ya no será el FIM debido a las fuerzas de inercia provenientes de arriba y de un posible deslizamiento de la Fundación. Además, incluso en el caso de una respuesta lineal y solo una zapata base con su masa (sin estructura arriba), el movimiento de la zapata no será exactamente el FIM debido a las fuerzas de inercia generadas por la masa de la zapata.

C. La  acción sísmica de input para el análisis de SSI utilizando el enfoque de subestructura (como se hace en SeismoStruct) puede consistir en uno de los siguientes:

• historial de aceleración en el nodo base fijo del macroelemento (este debería ser el FIM, a menudo se supone que es equivalente al movimiento de suelo, como ya se discutió), que luego se propagará a través del macroelemento y excitará las masas estructurales (incluida la massa de la zapata);

• Historiales de tiempo de fuerzas de inercia, calculadas como el producto de masas estructurales (incluidas las de la zapata) por la FIM, aplicadas a cada una de las masas de la estructura.

Se supone que estos dos enfoques de definición de input sísmico conducen a resultados de análisis idénticos en términos de desplazamientos relativos nodales (y, por lo tanto, deformaciones / esfuerzos materiales y fuerzas internas de los miembros). El primer enfoque es más fácil de aplicar porque solo se necesita definir un movimiento de base en los nodos fijos. Sin embargo, pueden aparecer problemas numéricos en casos especiales cuando las rigideces del macroelemento son muy grandes. El segundo enfoque es más difícil de aplicar, ya que uno tiene que aplicar un historial de tiempo de fuerza dinámica en todos los nodos con masas agrupadas y se vuelve engorroso cuando se usan masas distribuidas. Pero este método funciona en todos los casos.

Notas

1. Dado que el macroelemento SSI presenta una respuesta no lineal desde el comienzo del análisis, es muy importante aplicar la carga inicial en varios pasos para evitar la falta de convergencia o resultados erróneos. Por lo general, un número de pasos entre 50 y 100 debería ser suficiente, aunque en casos más exigentes de análisis podría ser necesario.

2. Se debe tener cuidado con el movimiento de tierra de entrada cuando se realiza un análisis dinámico ‘time-history’ con el macroelemento SSI. De hecho, dado que los dos nodos del macroelemento deben tener el mismo movimiento sin interacción inercial está presente, la forma mejor de realizar el análisis es imponiendo las fuerzas de inercia correspondientes en las masas estructurales de arriba y no imponiendo el historial de aceleración del movimiento del suelo en el nodo base.

Ejes Locales y Notación del Output