Curva de interacción suelo-estructura - ssi_py
Se trata de un modelo dinámico no lineal de interacción suelo-estructura (SSI), desarrollado e implementado por Allotey and El Naggar [2005a; 2005b], adecuado para el análisis de zapatas, muros de contención y pilotes sometidos a diferentes regímenes de carga (la nomenclatura seleccionada para esta curva pone en evidencia el hecho de que este modelo puede ser utilizado para llevar a cabo análisis laterales sobre pilotes, donde son comúnmente utilizadas las curvas p-y). El modelo tiene en cuenta la formación de brechas/aberturas (entre las fundaciones y el suelo circundante), con la opción de considerar también el "desplome" del suelo, presenta endurecimiento/degradación cíclico bajo cargas de amplitud variable, y puede modelar respuestas limitadas o no por las curvas principales iniciales. La degradación/endurecimiento cíclicos debidos a la presión de poros y a los cambios volumétricos son tenidos en cuenta mediante el uso de funciones de daño elípticas implementadas dentro del marco del modified rainflow counting algorithm [Anthes, 1997]; se utiliza también el enfoque del número equivalente de ciclos [por ej., Seed et al. 1975; Annaki and Lee, 1977]. Por otra parte, el efecto del desplome del suelo es modelado utilizando una función hiperbólica desarrollada empíricamente.
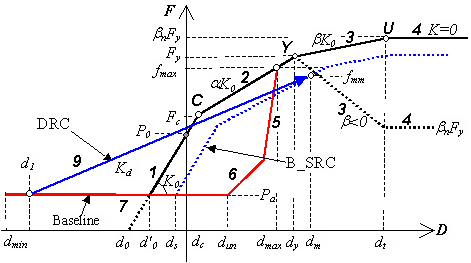
Resulta evidente que este modelo histerético por sí solo no es suficiente para modelar un determinado sistema de fundaciones. Por lo tanto, es necesario utilizar una serie de resortes (elementos link) caracterizados por una curva ssi_py adecuadamente calibrada, habitualmente en conjunto con un elemento viga-columna, de forma tal de representar el sistema de fundaciones requerido. En otras palabras, esta curva de respuesta ha de ser empleada dentro de la esfera del modelo de viga sobre una fundación Winkler no lineal (BNWF), en el cual se utiliza una serie de resortes bajo la fundación, a cada uno de los cuales debe asignársele una curva de respuesta. Para una zapata, los parámetros son los mismos para todos los resortes, mientras que para un pilote o muro de sostenimiento los parámetros cambian con la profundidad, debido al incremento de la sobrecarga.
Por otra parte, como se destaca aquí, es posible asignar un valor de amortiguamiento viscoso al elemento tipo link con el fin de representar de alguna forma los efectos del amortiguamiento por radiación (esto será similar a introducir un elemento dashpt en paralelo al resorte que modela el suelo). Los usuarios pueden consultar la literatura [por ej., Wolf, 1994; Allotey and El Naggar, 2005b] por indicaciones respecto a cómo calcular los valores apropiados de amortiguamiento, en función de las características vibratorias del sistema suelo-estructura. Habitualmente, si el período de vibración del sistema suelo-estructura es menor que aquel del sitio, los efectos del amortiguamiento por radiación pueden considerarse despreciables.
Para caracterizar por completo esta curva de respuesta es necesario definir diecinueve parámetros:
1º y 2º segmento de la curva
principal (K0,
Fc, Fy, ![]() )
)
El modelo idealiza las relaciones fuerza-desplazamiento del suelo
con curvas multi-lineales. El primer segmento de la curva principal
posee una rigidez inicial K0. El segundo
segmento de la curva comienza con una fuerza Fc (definida
como fracción de Fy),
con la rigidez reducida a ![]() . El segundo segmento
termina en correspondencia con la resistencia de cedencia del
suelo Fy. Los
parámetros de input varían en los rangos 0
. El segundo segmento
termina en correspondencia con la resistencia de cedencia del
suelo Fy. Los
parámetros de input varían en los rangos 0 ![]() Fc < 1, y 0.001
Fc < 1, y 0.001
![]()
![]()
![]() 1. Por defecto, Fc
= 0.5,
1. Por defecto, Fc
= 0.5, ![]() = 1, si se introducen
valores Fc
= 1, si se introducen
valores Fc
![]() 1 o
1 o ![]()
![]() 1 Fc y
1 Fc y ![]() son
reajustadas a sus valores por defecto.
son
reajustadas a sus valores por defecto.
3º y 4º segmento — curva final (![]() y
y
![]() )
)
El parámetro de rigidez ![]() (que define
la rigidez del tercer segmento en proporción a K0) y el parámetro de resistencia
(que define
la rigidez del tercer segmento en proporción a K0) y el parámetro de resistencia ![]() (que define la
resistencia última en función de Fy) determinan
el comportamiento final de la curva principal. La pendiente del
tercer segmento puede ser tanto positiva como negativa (comportamiento
de endurecimiento o de softening). La pendiente positiva no puede
ser mayor que la pendiente del segundo segmento, es decir que,
como requisito,
(que define la
resistencia última en función de Fy) determinan
el comportamiento final de la curva principal. La pendiente del
tercer segmento puede ser tanto positiva como negativa (comportamiento
de endurecimiento o de softening). La pendiente positiva no puede
ser mayor que la pendiente del segundo segmento, es decir que,
como requisito, ![]() <
<
![]() (el programa verifica que
(el programa verifica que ![]()
![]() 0.9
0.9![]() ). Para
). Para ![]() < 0, tel valor absoluto de la pendiente no puede
ser mayor que la pendiente inicial, es decir que
< 0, tel valor absoluto de la pendiente no puede
ser mayor que la pendiente inicial, es decir que ![]() .
.
El segundo tramo de la curva final siempre tiene pendiente nula.
La resistencia correspondiente al punto de cambio de pendiente
entre el tercer y cuarto segmento puede ser especificada mediante
el parámetro ![]() (
(![]()
![]() 0).
Más especificamente,
0).
Más especificamente, ![]() < 1 por
< 1 por ![]() < 0,
< 0, ![]() = 1 por
= 1 por ![]() = 0, y
= 0, y ![]() > 1 por
> 1 por ![]() > 0. Por defecto,
> 0. Por defecto,
![]() = 1 con
= 1 con ![]() =
0, y la curva final presenta un tramo horizontal. Si se ingresa
la combinación
=
0, y la curva final presenta un tramo horizontal. Si se ingresa
la combinación ![]() >
0 y
>
0 y ![]()
![]() 1 o viceversa,
ambos parámetros son reajustados a sus valores por defecto. En
el caso de una curva final con pendiente negativa (
1 o viceversa,
ambos parámetros son reajustados a sus valores por defecto. En
el caso de una curva final con pendiente negativa (![]() < 0), la respuesta resulta siempre limitada por
la curva principal inicial; es decir, se activa el marcador "/b",
independientemente de la definición por parte del usuario.
< 0), la respuesta resulta siempre limitada por
la curva principal inicial; es decir, se activa el marcador "/b",
independientemente de la definición por parte del usuario.
Fuerza inicial (P0)
y Fuerza Mínima (Pa)
La razón de fuerza inicial P0 y la razón
de fuera mínima Pa
tienen como fin representar la fuerza inicial presente antes del
comienzo de los ciclos y la fuerza mínima (activa) experimentada
para un desplazamiento negativo. Ambas son definidas en relación
a Fy. P0 varía entre 0 ![]() P0
P0
![]() 0.9. P0 > 0 traslada la curva principal hacia la
zona de tracción (hacia la izquierda) y especifica una fuerza
inicial para desplazamiento nulo. La fuerza mínima Pa es tratada como una línea de base en el modelo,
por lo que el movimiento nunca va por debajo de este nivel. Las
siguientes condiciones son aplicables a Pa: 0
0.9. P0 > 0 traslada la curva principal hacia la
zona de tracción (hacia la izquierda) y especifica una fuerza
inicial para desplazamiento nulo. La fuerza mínima Pa es tratada como una línea de base en el modelo,
por lo que el movimiento nunca va por debajo de este nivel. Las
siguientes condiciones son aplicables a Pa: 0 ![]() Pa
Pa ![]() P0 ; Pa
P0 ; Pa ![]()
![]() Fy
; Pa
Fy
; Pa ![]() Fc.
Fc.
Razón de fuerza de corte lateral (fs)
Este parámetro especifica la inclusión de una fuerza de corte lateral,
que es definida como fracción de sdFc (ver los parámetros
ps y es más adelante).
Este valor es tenido en cuenta sólo cuando el marcador "/s"
se encuentra activo, en cuyo caso se asume presente el corte lateral
y se tiene en cuenta fs
en vez de Pa
(es decir, Pa=0
y el eje de desplazamientos pasa a ser la línea base). Los límites
de fs son:
0 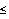 fs
fs
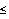 0.9.
0.9.
Parámetro de rigidez de descarga (![]() )
)
Dependiendo del marcador "/a", ![]() puede representar un límite al factor de degradación/endurecimiento
de la rigidez de descarga (marcador "/a" desactivado)
o especificar, en cambio, un multiplicador constante de la rigidez
de descarga (marcador "/a" activado). Cuando el marcador
se encuentra activado,
puede representar un límite al factor de degradación/endurecimiento
de la rigidez de descarga (marcador "/a" desactivado)
o especificar, en cambio, un multiplicador constante de la rigidez
de descarga (marcador "/a" activado). Cuando el marcador
se encuentra activado, ![]() varía como
varía como ![]() > 0; un valor
> 0; un valor ![]() > 1puede ser
utilizado para indicar una rigidez de descarga mayor que la rigidez
inicial de la curva principal inicial (el valor por defecto es
1).
> 1puede ser
utilizado para indicar una rigidez de descarga mayor que la rigidez
inicial de la curva principal inicial (el valor por defecto es
1).
Como se mencionó anteriormente, cuando el marcador se encuentra
desactivado, ![]() es
utilizado como valor límite del factor de rigidez de descarga
cíclica ku
(ver parámetros pk
y ek a continuación);
para degradación (pk<1),
pk
es
utilizado como valor límite del factor de rigidez de descarga
cíclica ku
(ver parámetros pk
y ek a continuación);
para degradación (pk<1),
pk 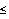
![]()
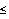 1,
mientras que para endurecimiento (pk>1),
1
1,
mientras que para endurecimiento (pk>1),
1 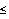
![]()
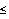 pk.
pk.
La mayoría de los experimentos no suelen arrojar valores de 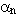 mucho
menores de uno, aunque esto se encuentra permitido en el modelo.
Es importante destacar que el valor de
mucho
menores de uno, aunque esto se encuentra permitido en el modelo.
Es importante destacar que el valor de 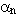 afecta
significativamente la respuesta calculada, por cuya razón su valor
debe ser seleccionado con cuidado; una estimación poco realista
de
afecta
significativamente la respuesta calculada, por cuya razón su valor
debe ser seleccionado con cuidado; una estimación poco realista
de 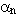 puede
conducir a resultados severamente erróneos.
puede
conducir a resultados severamente erróneos.
Parámetros de degradación/endurecimiento de la rigidez/resistencia
(pk, ek, ps, es)
Los parámetros de rigidez (pk, ek) y resistencia
(ps, es) son utilizados
para estimar el grado en el que los repetidos ciclos de carga
y descarga ocasionan degradación/endurecimiento de la rigidez
y la resistencia. Son utilizados en una forma "independiente
del esfuerzo" de la ecuación "elíptica" de degradación/endurecimiento
dada por Allotey
and El Naggar [2005a; 2005b] para calcular los factores de degradación/endurecimiento
de la rigidez y la resistencia, ku y sd. Los intervalos
de valores para estos parámetros son: pk>0,
ek>0 y ps>0, es>0; se obtiene degradación cuando pk o ps
son menores a 1; de lo contrario, se obtiene endurecimiento. Para
la mayoría de las aplicaciones prácticas, la degradación o el
endurecimiento ocurren simultáneamente tanto para la rigidez como
para la resistencia (es decir, es poco común que ocurra degradación
de la resistencia en simultáneo con endurecimiento de la rigidez,
o viceversa); sin embargo, esto no es impuesto.
Los factores ku
y sd son calculados
sobre la base de medio ciclo y son, por lo tanto, evaluados al
comienzo de cada descarga o recarga. Estos valores son aplicados
luego a la curva principal original para obtener ya sea la curva
estándar de recarga actual o la curva general de descarga. Las
siguientes limitaciones, algunas de las cuales ya han sido mencionadas
anteriormente, aplican como condiciones para los valores de estos
dos factores:
- para la descarga, sólo se tiene en consideración la degradación/endurecimiento de la rigidez, y para todos los casos sd=1
- para la descarga, cuando el marcador "/a" está
activado no ocurre degradación/endurecimiento cíclico de la
rigidez y se asume un factor de rigidez constante, es decir,
ku =
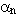
- para la descarga, cuando el marcador "/a" está
desactivado
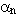 representa el
valor máximo/mínimo de degradación/endurecimiento, es decir
que si pk<1
entonces ku
representa el
valor máximo/mínimo de degradación/endurecimiento, es decir
que si pk<1
entonces ku
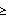
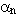 , mientras que si
pk>1
entonces ku
, mientras que si
pk>1
entonces ku
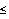
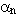
Nota: Por defecto, a todos estos parámetros se les asigna un valor igual a 1, lo cual significa que no ocurre ni degradación ni endurecimiento.
Parámetros de la curva S-N (ks,
f0)
La curva S-N describe la razón del esfuerzo cíclico (es decir,
la razón entre el esfuerzo cíclico y el esfuerzo efectivo medio
inicial ![]() )
respecto del número de ciclos de carga, en forma similar a aquella
utilizada en los análisis de fatiga. Es utilizada para evaluar
el daño incremental a cada semi-ciclo de carga, con el fin de
estimar la degradación/endurecimiento cíclico acumulativo al comienzo
de cada descarga o recarga. En el modelo, la curva S-N curve se
expresa como Sr
= S/S1 respecto
del número de ciclos, donde S y S1 son
las razones de esfuerzos para los ciclos actuales y primero, respectivamente.
Hay, a disposición del usuario, dos formas diferentes de la curva
S-N: si el marcador "/logS" está activado se utiliza
una relación log-log, mientras que si el marcador "/logS"
está desactivado se considera en cambio una relación semi-log.
El parámetro ks
es la pendiente de la curva S-N; para la relación log-log, ks es igual a la pendiente
de la curva S-N convencional (ksc), mientras
que para el caso semi-log, ks = ksc/S1 [ver Allotey
and El Naggar, 2005a; 2005b].
)
respecto del número de ciclos de carga, en forma similar a aquella
utilizada en los análisis de fatiga. Es utilizada para evaluar
el daño incremental a cada semi-ciclo de carga, con el fin de
estimar la degradación/endurecimiento cíclico acumulativo al comienzo
de cada descarga o recarga. En el modelo, la curva S-N curve se
expresa como Sr
= S/S1 respecto
del número de ciclos, donde S y S1 son
las razones de esfuerzos para los ciclos actuales y primero, respectivamente.
Hay, a disposición del usuario, dos formas diferentes de la curva
S-N: si el marcador "/logS" está activado se utiliza
una relación log-log, mientras que si el marcador "/logS"
está desactivado se considera en cambio una relación semi-log.
El parámetro ks
es la pendiente de la curva S-N; para la relación log-log, ks es igual a la pendiente
de la curva S-N convencional (ksc), mientras
que para el caso semi-log, ks = ksc/S1 [ver Allotey
and El Naggar, 2005a; 2005b].
El parámetro f0
es el esfuerzo del suelo correspondiente a S1,
es decir, f0
= S1![]() (debe
notarse que las unidades de
(debe
notarse que las unidades de ![]() deben ser consistentes
con las de Fy).
El parámetro varía como f0>0,
con un valor por defecto de f0=2Fy, y puede ser ajustado
para tener en cuenta los efectos del esfuerzo cíclico medio [por ej., Hyodo
et al., 1994].
deben ser consistentes
con las de Fy).
El parámetro varía como f0>0,
con un valor por defecto de f0=2Fy, y puede ser ajustado
para tener en cuenta los efectos del esfuerzo cíclico medio [por ej., Hyodo
et al., 1994].
Parámetros de fisuración del suelo (p1,
p2)
El parámetro de la fuerza de abertura, p1,
es utilizado para estimar el punto de recarga directa (fmm) al cual es dirigida
la curva de recarga directa (DRC). El valor de este parámetro
varia entre 0 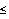 p1
p1 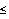 1,
siendo la DRC paralela al eje de desplazamientos cuando p1=0, como fue mencionado
anteriormente. Para la recarga luego del movimiento a lo largo
de la línea de base cuando el marcador "/s" se encuentra
activado, esto se traduce en la formación de una abertura pura.
El paso de la curva de recarga directa (DRC) a la curva de recarga
estándar (SRC) tiene lugar en la intersección de la DRC y la curva
de recarga estándar de base (B_SRC). Por mayores detalles, los
usuarios pueden consultar el trabajo de Allotey
and El Naggar [2005a; 2005b]. El valor por defecto es p1=0, es decir, se
asume comportamiento completamente no confinado (esto representa,
por ejemplo, la respuesta de abertura completa entre un pilote
y una arcilla dura).
1,
siendo la DRC paralela al eje de desplazamientos cuando p1=0, como fue mencionado
anteriormente. Para la recarga luego del movimiento a lo largo
de la línea de base cuando el marcador "/s" se encuentra
activado, esto se traduce en la formación de una abertura pura.
El paso de la curva de recarga directa (DRC) a la curva de recarga
estándar (SRC) tiene lugar en la intersección de la DRC y la curva
de recarga estándar de base (B_SRC). Por mayores detalles, los
usuarios pueden consultar el trabajo de Allotey
and El Naggar [2005a; 2005b]. El valor por defecto es p1=0, es decir, se
asume comportamiento completamente no confinado (esto representa,
por ejemplo, la respuesta de abertura completa entre un pilote
y una arcilla dura).
El parámetro p2
representa el efecto del "desplome" del suelo, y es
utilizado para estimar el desplazamiento inicial, ds, de la B_SRC actual. Este parámetro varía de
la siguiente forma: 0 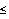 p2, con p2=0, lo cual significa que no tiene lugar ningún
desplome (es decir, la B_SRC comienza a partir del punto actual
de desplazamiento de descarga de la línea de base); ésta es la
hipótesis por defecto.
p2, con p2=0, lo cual significa que no tiene lugar ningún
desplome (es decir, la B_SRC comienza a partir del punto actual
de desplazamiento de descarga de la línea de base); ésta es la
hipótesis por defecto.
Combinación de los ajustes de marcadores
Como se describió anteriormente, esta curva de respuesta hace uso
de cinco marcadores (/logS, /s, /b, /kbu, /a) que pueden ser utilizados
para activar/desactivar un número igual de funcionalidades en
el modelo, también descritas anteriormente. A cada uno de los
cinco marcadores puede asignársele uno de dos estados mutuamente
excluyentes (activado (o) o desactivado
(x)), por lo cual existe un total de 2^5=32
combinaciones posibles de ajustes de marcadores, como se muestra
en la tabla a continuación. Por defecto se utiliza la combinación
nº 31, lo cual significa que todos los marcadores están activados,
es decir que (i) se considera una curva S-N log-log, (ii)
se incluye corte lateral, (iii) la respuesta es limitada, (iv)
la rigidez de descarga sigue la curva principal, y (v) no ocurre
degradación/endurecimiento cíclico de la rigidez.
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
21
|
22
|
23
|
24
|
25
|
26
|
27
|
28
|
29
|
30
|
31
|
|
| /logS |
x
|
x
|
x
|
x
|
x
|
x
|
x
|
x
|
x
|
x
|
x
|
x
|
x
|
x
|
x
|
x
|
o
|
o
|
o
|
o
|
o
|
o
|
o
|
o
|
o
|
o
|
o
|
o
|
o
|
o
|
o
|
o
|
| /s |
x
|
x
|
x
|
x
|
x
|
x
|
x
|
x
|
o
|
o
|
o
|
o
|
o
|
o
|
o
|
o
|
x
|
x
|
x
|
x
|
x
|
x
|
x
|
x
|
o
|
o
|
o
|
o
|
o
|
o
|
o
|
o
|
| /b |
x
|
x
|
x
|
x
|
o
|
o
|
o
|
o
|
x
|
x
|
x
|
x
|
o
|
o
|
o
|
o
|
x
|
x
|
x
|
x
|
o
|
o
|
o
|
o
|
x
|
x
|
x
|
x
|
o
|
o
|
o
|
o
|
| /kbu |
x
|
x
|
o
|
o
|
x
|
x
|
o
|
o
|
x
|
x
|
o
|
o
|
x
|
x
|
o
|
o
|
x
|
x
|
o
|
o
|
x
|
x
|
o
|
o
|
x
|
x
|
o
|
o
|
x
|
x
|
o
|
o
|
| /a |
x
|
0
|
x
|
o
|
x
|
o
|
x
|
o
|
x
|
o
|
x
|
o
|
x
|
o
|
x
|
o
|
x
|
o
|
x
|
o
|
x
|
o
|
x
|
o
|
x
|
o
|
x
|
o
|
x
|
o
|
x
|
o
|
Notas
- Este versátil modelo histerético se encuentra aún en etapa de evaluación y mayor desarrollo. Por ejemplo, esta curva ssi_py es apta sólo para la dirección fuerza-desplazamiento normal (es decir, no da cuenta de la respuesta tangencial fuerza-deslizamiento). Además, los grados de libertad no se encuentran completamente acoplados (una limitación que es también consecuencia de la actual naturaleza desacoplada de los elementos link en SeismoStruct). El tratamiento de estos temas está contemplado para futuras versiones de SeismoStruct.
- Es muy posible que futuras versiones de SeismoStruct introduzcan una forma significativamente más amigable de calibrar/ajustar los parámetros de esta curva de respuesta, mediante el uso de menúes desplegables y/o botones de selección para especificar las diferentes opciones de modelado.
- En los últimos años se ha propuesto un enfoque alternativo para el modelado de sistemas de fundación, que consiste en el empleo de un modelo macro V-H-M (vertical-horizontal-rotación) completamente acoplado [por ej., Cremer at al, 2002]. Este modelo utiliza sólo un elemento para modelar toda la respuesta de la fundación y está basado sobre una formulación plástica de la superficie de fluencia. Aunque se trata, sin dudas, de un enfoque prometedor para el modelado de la interacción suelo-estructura, se considera que, dado el estado actual de desarrollo y práctica, el tradicional método BNWF, implementado actualmente en SeismoStruct mediante la utilización de la poderosa curva de respuesta ssi_py, provee al usuario todas las funcionalidades necesarias para el modelado adecuado de la interacción estática y, sobre todo, dinámica entre suelos, fundaciones y estructuras.