Análisis de Pandeo

En general, para identificar el punto límite que reconoce la transición de una estructura estable a una inestable, se debe realizar un análisis incremental. El análisis incremental considera las no linealidades geométricas y las no linealidades de materiales. En algunos casos, es decir, estructuras de acero delgadas, la estabilidad se rige por las no linealidades geométricas. Por lo tanto, descuidando el comportamiento del material no lineal y suponiendo que la distribución relativa de la fuerza interna sea igual en todas las proporciones de la carga aplicada, se puede realizar un análisis de pandeo en lugar del incremental. Además de estos dos supuestos, las matrices de rigidez geométrica del elemento son funciones lineales de las fuerzas a su extremos. Por lo tanto, estas hipótesis permiten escribir la ecuación de rigidez global en forma de un problema de Eigenvalores generalizado en que la ecuación de equilibrio en el estado crítico es:

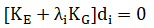
K_E es la matriz de rigidez lineal elastica. K_G es la matriz de rigidez geométrica que representa el cambio en la rigidez que resulta de los cambios en la geometría a medida que aumenta la carga aplicada. Se calcula para un patrón de carga de referencia P_ref que corresponde al estado básico de la estructura con precargas. λ_i es un vector de factores de carga (eigenvalores) con respecto a P_ref  y di es la forma del modo de pandeo (eigenvectores), donde i se refiere al el i modo de pandeo. El valor más bajo de λ_i produce el vector de carga crítica elástica λ_min P_ref. Comúnmente, es más fácil resolver este tipo de problema que resolver un análisis incremental.