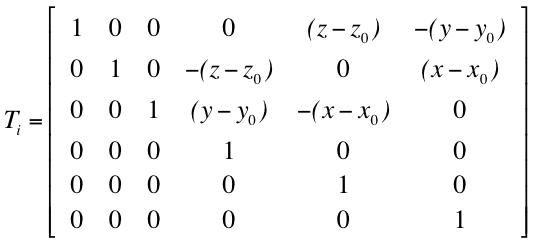Modal/Mass quantities

This module is visible only when eigenvalue or adaptive pushover  analyses have been carried out. It is also shown with a different name 'Eigenvalue Results', in the case of Pushover analysis when the Target displacement is calculated, providing a summary of (i) the main eigenvalue results (i.e. the natural period/frequency of vibration of each mode, the modal participation factors and the effective modal masses), and (ii) the nodal masses. These results can be easily copied to a text editor, through the right-click popup menu.

Regarding the nodal masses, SeismoStruct provides a table in which are summarized the masses of the nodes for each degree of freedom (also for rotation). For a particular node, the rotational mass is computed as the rotational mass defined by the user for that node, plus the translational mass at that node times the square of the distance to the centre of gravity of the model.

The Modal Participation Factors, obtained as the ratio between the modal excitation factor () and the generalised mass (), provide a measure as to how strongly a given mode n participates in the dynamic response of a structure. However, since mode shapes can be normalised in different ways, the absolute magnitude of the modal participation factor has in effect no meaning, and only its relative magnitude with respect to the other participating modes is of significance [Priestley et al., 1996].

For the above reason, and particularly for the case of buildings subjected to earthquake ground-motion, it is customary for engineers/analysts to use the effective modal mass () as a measure of the relative importance that each of the structure's modes has on its dynamic response. Indeed, since meff,n can be interpreted as the part of the total mass M of the structure that is excited by a given mode n, modes with high values of effective modal mass are likely to contribute significantly to response, whilst the inverse is also true.

Notes

1. Users are advised to refer to the available literature [e.g. Clough and Penzien, 1993; Chopra, 1995] for further information on modal analysis and respective parameters.
2. The mode shapes are normalised so that Φn=1.
3. MPFs for rotations are calculated considering a transformation matrix defined as follows (where x0, y0, z0 are the coordinates of the centre of mass), so that the modal excitation factor becomes 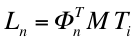, from which the effective modal mass (as for the translational DOFs).