Masonry Elements (NTC-18)

All the masonry element checks (shear capacity, bending moment and drift) should be carried out for all the elements of every floor, according to sections 7.8.2.2 and 7.8.3.2 of NTC-18 and section C8.7.1.3.1.1 of Commentary of NTC-18.

Shear Force Capacity
The shear force capacity of unreinforced masonry walls controlled by flexure under an axial load N is calculated according to the following expression:

Unreinforced Masonry Walls
Mohr-Coulomb equation, as described in section 7.8.2.2.2 of NTC-18 and section 6.2 of EC6, for masonry with blocks

Turnšek-Čačovič equation, as described in section C8.7.1.3.1.1 of commentary of NTC-18, for irregular masonry (irregular stones) and for existing regular masonry (bricks, regular stones):

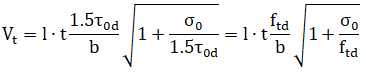
Mann-Müller equation, as described in section C8.7.1.3.1.1 of commentary of NTC-18)for existing regular masonry (bricks, regular stones):

In some cases, it is necessary to take the lower value between the different expressions above. For example, in the case of Unreinforced Masonry Wall with bricks the Commentary of the NTC-18 requires to take the lower value between the Turnšek-Čačovič and Mann-Müller criterion.

Reinforced Masonry Walls
The shear capacity of reinforced masonry walls is calulcated, according to section 7.8.3.2.2 of NTC-18, as the sum of the contribution of masonry (V_t,M) and of the reinforcement (V_t,S), as shown in the following expression:

where:

and

Further, the shear capacity should not exceed the following value:

Users are advised to refer to the Code for the definition of the parameters and further details on the expressions.

Bending Moment Capacity
The Bending moment capacity of unreinforced masonry walls calculated according to the following expression:

The Bending moment capacity of unreinforced masonry spandrels calculated according to the following expression:

The Bending moment capacity of masonry walls and spandrels with reinforcement is calculated based in the following expression of section 9.3.5.2 of TMS 402:

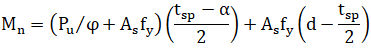
where

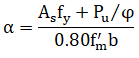
The above equations are valid for both centered and noncentered flexural reinforcement. In the case of centered flexural reinforcement, d=t_sp/2, the bending moment capacity is obtained as:

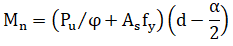
Users are advised to refer to the Code for the definition of the parameters and further details on the expressions.

Drift
The capacity of masonry walls may be expressed in terms of drift. The drift for masonry walls controlled by flexure is taken equal to 0,01 for walls without reinforcement and 0,016 for walls with reinforcement, according to sections 7.8.2.2.1 and 7.8.3.2.1 of NTC-18. Further, the drift for masonry walls controlled by shear is taken equal to 0,005 for walls without reinforcement and 0,008 for for walls with reinforcement, according to section 7.8.2.2.2 and 7.8.3.2.2 of NTC-18.