Pile Foundations macro-element - ssilink2
This element extends the nonlinear macro-element approach to the analysis of laterally loaded flexible piles and soil-pile-structure interaction. It is based on the work of Correia and Pecker [2019b]. The lateral response of the entire soil-pile system to seismic actions is thus condensed at the pile-head, being represented by a zero-length element located at the base of the columns and subjected to the foundation input motion, as shown in the Figure below:
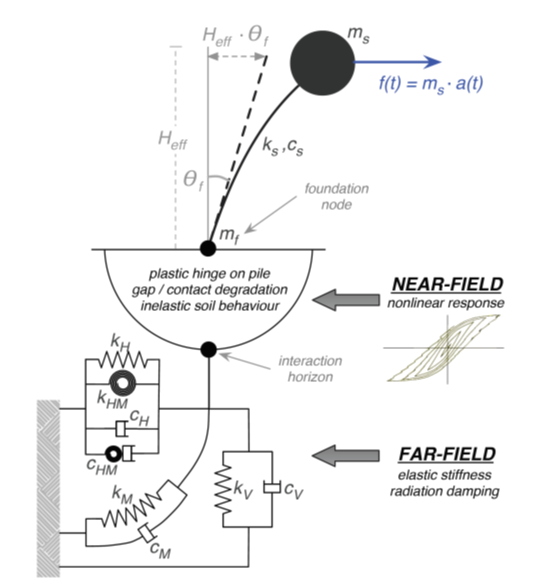
The pile-head macro-element model represents the lateral behaviour of single vertical piles, subjected to a horizontal load and a moment, from the initial stages of loading up until reaching failure. The effects of vertical loading are not directly considered in this model except for its influence on the plastic moment of the pile cross-section. Otherwise, it is considered that the upper zone of the soil profile, until the depth at which the plastic hinge will form, only contributes to the lateral load resistance. The vertical load is assumed to be transferred to the surrounding soil below that depth, where there is no influence of gap opening.
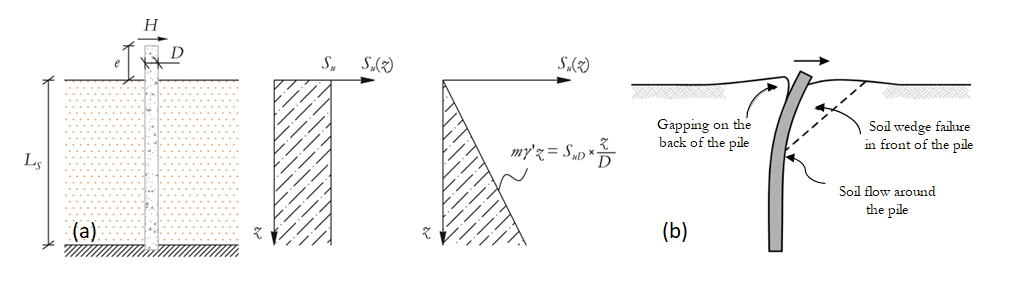
A saturated soil deposit is considered and, upon seismic motion, it is assumed to be impervious. The soil is thus considered to have undrained behaviour since the aim of the macro-element is to simulate the pile response under seismic actions, or short-term cyclic loads, and the Tresca failure criterion is assumed to be valid. In the Figure below, Figure a represents the two simplified geotechnical scenarios considered, in terms of undrained shear strength (Su) distribution along the depth of the soil deposit: constant or linear. Figure b illustrates the characteristic soil response for a laterally loaded long pile, namely: a soil passive wedge failure at shallow depths and flow-around failure at larger depths, with a possible gap formation at the back of the pile.
The proposed macro-element is based on the three major features of the behaviour of laterally loaded piles, namely:
i) Initial elastic response,
ii) Gap opening and closure,
iii) Failure loading conditions.
The bounding surface plasticity model is used to represent a continuous transition between the initial elastic response and the plastic flow at failure, for monotonic as well as cyclic pile-head loading conditions. The gapping behaviour is represented by a nonlinear elastic model which, however, takes into account and is influenced by the plastic deformation state in the surrounding soil.
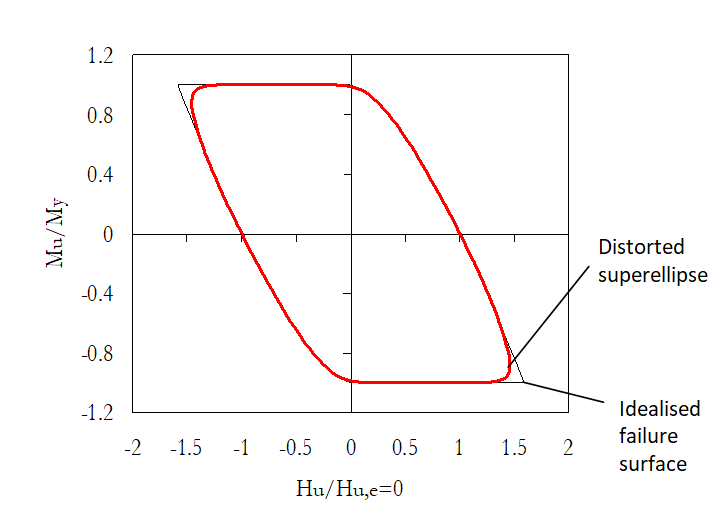
The bounding surface in the macro-element model corresponds to the failure surface for laterally loaded piles. Since there is no evidence showing that non-associative behaviour should be considered, associative plasticity is used and the bounding surface acts simultaneously as the plastic potential surface. No axial load effects are considered in this macro-element formulation and, consequently, the failure surface is defined in the loading space of the pile-head horizontal force and moment only. Furthermore, a planar loading is assumed.
A “rounded” approximate failure surface was proposed in Correia and Pecker [2019a], which is based on the so-called superellipse. Supposing a superellipse centred at the point (Hc, Mc), with a horizontal axis length and a vertical axis length My, which is also superimposed to a distortion of its shape, g< 0, this approximate failure surface can be expressed as:
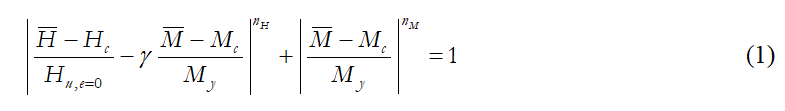
The positive exponents nH and nM control the curvature of the sides of the superellipse. The Figure below represents such distorted superellipse configuration, centred at the origin (Hc = Mc = 0), with its parameters calibrated in order to fit the failure surface for the linear Su soil profile.
Twenty three parameters are required for the definition of the macro-element model:
- The Pile Diameter (DIAM)
- The Pile Stiffnesses for vertical, horizontal and rotational directions (K_VV, K_HH, K_MM, K_HM, K_TT)
- The Pile Capacity (QQ_H_MAX, QQ_M_MAX)
- The Superelipse BS parameters (Exp_nH,Exp_nM, GAMMA)
- The Maximum Gap depth (ZW)
- The Pile Flexural Stiffness (Eplp)
- The Gap Evolution Parameter (BETA)
- The Minimum Gap Evolution Parameter (ETA)
- The Reference plastic modulus parameter (PL_H0)
- he exponent for plastic modulus evolution (PL_nur)
- The Lower limit value for delta in unloading/reloading (Delta_LIM)
The pile flexural stiffness, Eplp can be easily computed, while the pile yield moment, My, can be computed using any cross-section analysis tool (and considering the static vertical load on the pile). On the other hand, formulas for Hu, e=0 and zw, are derived in Correia and Pecker [2019a].
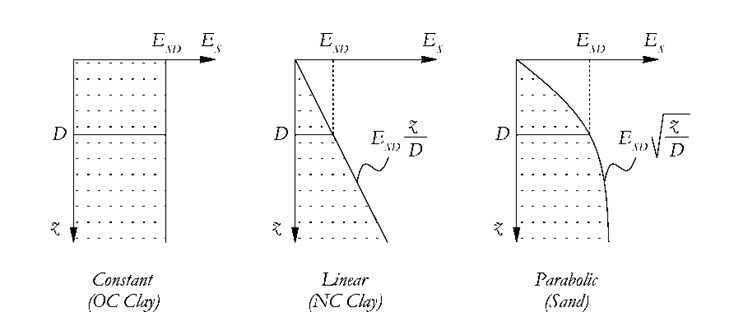
Gazetas [1991] provides formulas for a direct computation of pile-head lateral and axial stiffness and damping coefficients. These are valid for soil profiles with constant, linear or parabolic increase of soil stiffness with depth, which are representative of OC clay, NC clay and sand, respectively. The Figure below represents the soil stiffness evolution with depth in such idealised soil profiles.
His expressions for pile-head static stiffnesses have been adopted, with slight modifications, in the current version of EC 8 – Part 5 [2003]. These are valid for flexible or long piles and are summarised in the Table below.

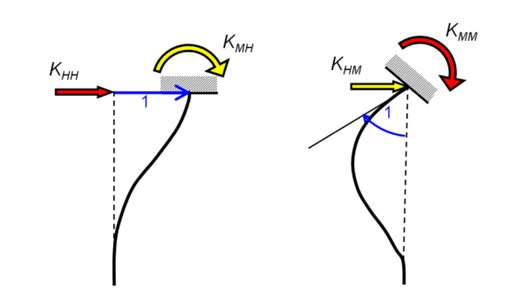
In those expressions, D is the pile diameter, ESD is the soil modulus of deformation at a depth equal to the pile diameter and Ep is the Young’s modulus of the pile material. The pile-head stiffness matrix components follow the sign convention expressed in the Figure below.
Gazetas [1991] also presents the corresponding pile-head damping coefficients, which are computed for each frequency f according to the expressions in the table below.
The dynamic components of the pile-head stiffnesses have been shown by Gazetas [1984] to be roughly equal to one, for the usual frequency range of interest for structural response. Hence, pile-head static stiffnesses may be approximately used as dynamic ones, for single flexible piles. Variation of the damping ratio components with frequency is linear, as predicted by the expressions in the Table below. This means that radiation damping behaviour may be approximated by physical dashpots with constant damping coefficient C.

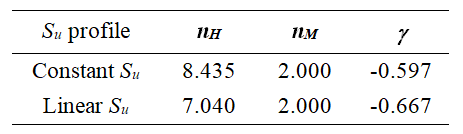
The bounding surface parameters are fixed for each of the soil strength profiles and are shown in the Table below. The limit value dLim is a parameter related to the numerical convergence and varies between 0.01 and 0.2, with a default value of 0.1.
Finally, the remaining 4 calibration parameters, 2 of them are related to monotonic response –b and , and the 2 others are related to cyclic behaviour –h and nUR. Alternatively, 2 of the parameters are related to the gapping behaviour –b and h, and 2 others are related to the plasticity model – and nUR. The parameters b, and nUR are always positive, while h can also be equal to zero if no residual gap opening is considered. Their default values and ranges of variation are presented in the table below

Note: Care should be taken on the ground motion input when a dynamic time history analysis with the SSI macro-element is made. In fact, given that the two nodes of the macro-element should have the same motion while no inertial interaction is present, the soundest way of performing the analysis is not by imposing the ground motion acceleration history at the base node but by imposing the corresponding inertia forces on the structural masses above.
Some theoretical background on SSI analysis
SSI analysis can be carried out through the employment of a nonlinear solid finite element model (i.e. soil-block), or by means of a simpler and thus more practical substructure approach, which is the one that can be adopted in SeismoStruct.
In principle, when modelling SSI using the substructure method, one should first analyse the kinematic interaction with the full model of the soil and the structure, with the structural stiffness but no structural mass. In such procedure, the seismic input propagation in the soil is explicitly modelled, typically in the frequency domain (though not necessarily), and the end result is the foundation input motion (FIM), i.e. the motion of the foundation if it were massless. This initial step is, however, often avoided by assuming that the kinematic interaction may be neglected and thus using the free-field ground motion as the FIM (this free-field motion is also often assumed to result only from the vertical propagation of shear waves through horizontal soil layers).
A second stage in the modelling of SSI using the substructure method would then be the calculation of the foundation impedances (i.e. dynamic response properties of the foundation), typically represented by a set of springs, dashpots (and possibly fictitious masses to get the correct frequency-dependence of the impedances). This second step may be simplified by determining the impedances from existing expressions in the literature.
The final step is the analysis of the structure, with its stiffness and mass, supported on the foundation impedances and subjected to the FIM. This is what can be done in SeismoStruct, which features the added advantage of being able, through the employment of the SSI macro-element, of considering also the nonlinear response of the foundation system. In other words, an SSI analysis carried out using this macro-element corresponds to a hybrid approach in-between the inertial interaction analysis of the substructure approach, which is strictly valid only for linear response, and a nonlinear solid finite element modelling of SSI effects.
Within the context defined above, therefore, the following should be kept in mind by the user:
- The substructure method is only theoretically correct if the response is linear, i.e. without sliding or uplifting of a footing, gapping of a pile, stiffness degradation, plastic behaviour, and irrecoverable displacements; in the presence of nonlinearities, therefore, this type of analysis inevitably involves some degree of approximation.
- As already noted, the FIM is the input motion that the foundation would have only if it were massless (as well as the rest of the structure) and if it would behave linearly. Indeed, and for instance, if the foundation model of a footing simulates its sliding resistance, and if there is structural mass, the motion of the foundation will no longer be the FIM because of the inertial forces coming from above and from a possible sliding of the foundation. Moreover, even in the case of linear response and just a footing with its mass (no structure above), the motion of the foundation will not be exactly the FIM because of the inertia forces generated by the footing mass.
- The seismic input for SSI analysis using the substructure approach (as done in SeismoStruct) can consist of one of the following:
- acceleration time-history at the fixed base node of the macro-element (this should be the FIM, often assumed to be equivalent to the free-field motion, as discussed already), which will then propagate through the macro-element and excite the structural masses (including the foundation one);
-
inertia forces time-histories, computed as the product of structural masses (including the foundation one) by the FIM, applied to each of the masses of the structure.
These two seismic input definition approaches are supposed to lead to identical analysis results in terms of nodal relative displacements (and hence material strains/stress and member internal forces). The first approach is easier to apply because only a base motion in the fixed nodes needs to be defined. However, it may give rise to numerical problems in special cases when the stiffnesses of the macro-element are very large. The second approach is more difficult to apply, because one has to apply a dynamic force time-history in all nodes with lumped masses and becomes cumbersome when distributed masses are used. But this method works in all cases.
Local Axes and Output Notation