Elastomeric Isolator 1 Element (Bouc Wen) - isolator 1

Isolator 1 Elements are 3D elements with zero length used to model the behaviour of elastomeric isolators used in Seismic Isolation Applications. Isolator 1 Elements have coupled plasticity properties for the two shear directions (axes 2 and 3 in the local coordinate system of the isolator 1 element) while they are characterised by linear elastic behaviour for the remaining four deformation types. The behaviour in the shear directions is based on the hysteretic behaviour proposed by Wen [1976] and Park et al. [1986]. In the shear directions the force-deformation relationships follow the equations below:

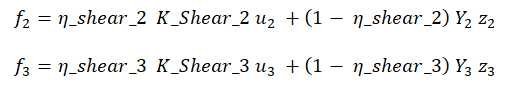
where η_shear_2 and η_shear_3 are the ratios of the Post Yield Stiffness to the Elastic (Pre-Yielding) Stiffness of the isolator in each shear direction (Isolator Hardening Ratios), K₂ and K₃ are the elastic Stiffnesses of the isolator in each direction, Y₂ and Y₃ the yielding deformations in each shear direction while z₂ and z₃ are internal hysteretic variables.

Thirteen parameters are needed in order to describe the isolator 1 element behaviour:

Elastic Stiffness in the axial (local axis 1) direction - K_axial
Linear elastic response of the isolator is considered in the axial direction

Elastic Stiffness in the shear (local axis 2 and 3) directions - K_shear_1, K_shear_2

Elastic Stiffnesses in the torsional and rotational degrees of freedom - Ktorsional, Krot1, Krot2
Linear elastic response of the isolator is considered in the torsional and rotational degrees of freedom.

Isolator Characteristic Strength for each shear direction – fy_shear_1, fy_shear_2

Isolator Hardening ratio for each shear direction – η_shear_1, η_shear_2

Variable controlling the hysteresis Amplitude - A

hysteretic shape variable - β

hysteretic shape variable - γ

In this element's dialog box it is also possible to define an element-specific damping, as opposed to the global damping described in here. To do so, users need simply to press the Damping button and then select the type of damping that better suits the element in question (users should refer to the Damping menu for a discussion on the different types of damping available and hints on which might the better options). Users are reminded also that damping defined at element level takes precedence over global damping, that is, the "globally-computed" damping matrix coefficients that are associated to the degrees-of-freedom of a given element will be replaced by coefficients that will have been calculated through the multiplication of the mass matrix of the element by a mass-proportional parameter, or through the multiplication of the element stiffness matrix by a stiffness-proportional parameter, or through the calculation of an element damping Rayleigh matrix.

Note: In general the rule A/(β+γ) = 1 should be followed when defining the model hysteretic variables

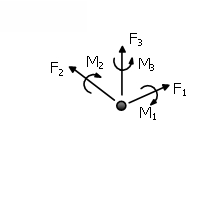
Local Axes and Output Notation