Buckling Analysis

In general, in order to identify the limit point that recognises the transition from a stable to an unstable structure, an incremental analysis should be performed. The incremental analysis considers both geometric and material nonlinearities. In some cases, i.e. slender steel structures, the stability is governed by the geometric nonlinearities. Hence, neglecting nonlinear material behaviour and assuming the relative distribution of internal force equal at all ratios of the applied load, a buckling analysis can be performed in place of the incremental one. Besides at these two assumptions, the element geometric stiffness matrices are linear functions of their end forces. Hence, these hypothesis permit to write the global stiffness equation in the form of a generalised eigenvalue problem in which the equation of equilibrium at the critical state is

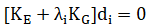
K_E is the linear elastic stiffness matrix. K_G is the geometric stiffness matrix which represents the change in stiffness that results from changes in geometry as the applied loading is increased. It is computed for a reference loading pattern P_ref which corresponds to the base state of structure with preloads. λ_i is a vector of load factors (eigenvalues) with respect to P_ref and d_i is the buckling mode shape (eigenvectors), where i refers to the ith buckling mode. The lowest value of λ_i provides the elastic critical load vector λ_min P_ref. Commonly, it is easier to solve this kind of problem than to solve an incremental analysis.