Inestabilidad numérica, divergencia y predicción de la iteración

Además de la verificación de la convergencia, es posible realizar otras tres verificaciones de la solución al final de cada incremento del proceso iterativo: inestabilidad numérica, divergencia de la solución y predicción de la iteración. Estos criterios (todos ellos basados en fuerzas/momentos) tienen como fin evitar el cálculo de iteraciones de equilibrio inútiles en los casos en los cuales resulta evidente que la convergencia no será alcanzada, minimizando así la duración del análisis.

Inestabilidad Numérica
La posibilidad de que la solución devenga en numéricamente inestable es controlada en cada iteración mediante la comparación de la norma Euclidiana de las cargas no equilibradas, Gnorm, con una tolerancia máxima predefinida (por defecto=1.0E+20), varios órdenes de magnitud mayor que el vector de carga aplicado. Si Gnorm excede esta tolerancia, se asume que la solución es numéricamente inestable y las iteraciones del incremento actual son interrumpidas, con un mensaje del marcador del registro igual a Max_Tol.

En ocasiones, modelos muy inestables pueden conducir al desarrollo de fuerzas no equilibradas varios órdenes de magnitud mayores que el valor máximo de tolerancia. Esto genera, a su vez, un Problema de Solución (es decir, el análisis se detiene, aunque de forma "prolija"), y las iteraciones del incremento actual son interrumpidas, con un mensaje del marcador del registro igual a Sol_Prb.

Divergencia de la solución
La divergencia de la solución es controlada mediante la comparación entre el valor de Gnorm obtenido en la iteración actual y aquel obtenido en la iteración anterior. Si Gnorm ha aumentado, se asume que la solución está divergiendo, por lo que se interrumpen las iteraciones del incremento actual, con un mensaje del marcador del registro igual a Diverge.

Predicción de la iteración
Finalmente, se lleva a cabo también un control de la tasa logarítmica de convergencia, con el fin de predecir el número de iteraciones (itepred) requeridas para alcanzar la convergencia. Si itepred es mayor que el número máximo de iteraciones especificado por el usuario, se asume que la solución no convergerá y se interrumpen las iteraciones del incremento actual, con un mensaje del marcador del registro igual a Prd_Ite.

Para calcular el valor de itepred se utiliza la siguiente ecuación, en la cual ite representa el número actual de iteraciones y Gtol es la tolerancia de fuerzas/momentos:

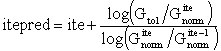
Las tres verificaciones descritas anteriormente son habitualmente confiables y efectivas dentro del ámbito de aplicabilidad de SeismoBuild, siempre y cuando los controles de divergencia y de predicción de la iteración no sean llevados a cabo durante las primeras iteraciones de un incremento, durante las cuales la solución puede no ser suficientemente estable aún. Pueden encontrarse más detalles sobre este tema en la sección acerca de la estrategia iterativa, en la cual se describen todos los parámetros relacionados con estos criterios

Nota: Cada elemento con formulación basada en fuerzas requiere un cierto número de iteraciones para alcanzar el equilibrio interno. En algunos casos, el equilibrio interno no puede ser alcanzado, lo cual es señalado por los mensajes del marcador del registro fbd_inv y fbd_ite. Por mayor información sobre este tema, por favor dirigirse aquí.