Elastik olmayan dolgu panel elemanı - infill

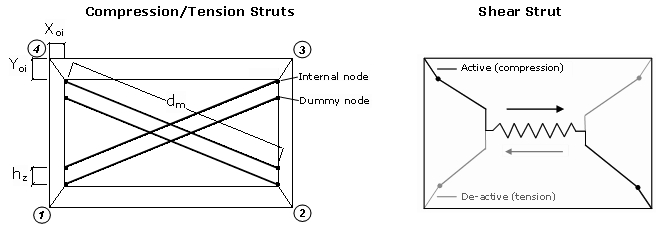
Çerçeveli yapılardaki dolgu panellerin doğrusal olmayan davranışlarını modellemek için Crisafulli [1997] tarafından geliştirilen ve ilk kez programlanan dört düğüm noktalı yığma panel elemanı, Blandon [2005] tarafından SeismoStruct'a uygulandı. Her panel altı çubuk tarafından temsil edilmektedir; her iki diyagonal yönde, iki çapraz köşe arasında eksenel yükü taşımak için ikişer paralel çubuk ve panelin üstünden altına kadar kesme kuvvetini taşımak için bir üçüncü çubuk bulunmaktadır. Bu sonuncu çubuk sadece basınçta olan diyagonal boyunca çalışır, dolayısıyla "etkinleştirilmesi" panelin deformasyonuna bağlıdır. Eksenel yük çubukları yığma çubuk histeretik modelini kullanırken, kesme çubuğu özel iki doğrulu histeretik kuralını kullanır.

Ayrıca, aşağıdaki figürde gözlendiği üzere, çerçeve ve dolgu paneli arasındaki gerçek teması hesaba katmak için dört dahili düğüm noktası kullanılırken (yani, kolonların ve kirişlerin sırasıyla genişlik ve yüksekliklerini hesaba katmak için), çerçeve ve dolgu panel arasındaki temas uzunluğunu hesaba katmak amacıyla dört dummy (sahte) düğüm noktası tanımlanır. Tüm iç kuvvetler elemanın çerçeveye bağlandığı dört dış düğüm noktalarına dönüştürülür (burada belirtildiği gibi, bu noktalar saat yönünün tersi sırasında tanımlanmalıdır).

Note: Dolgu duvar elemanları, yukarıda belirtildiği gibi çerçeve yapılardaki dolgu duvar etkisini hesaba katmak için modellense de, döşemelerdeki rijitlik katkılarını ve elastic olmayan davranış şablonlarını da akıllı bir şekilde taklit etmek için de kullanılabilirler. İstenen davranış, uygun özelliklere sahip bu eleman tiplerini ve/veya inelastic çubuk (kafes) eleman tiplerini stratejik olarak konumlandırılarak elde edilebilir (bkz. ilgili forum başlığı).

Bu tür bir elemanın tam olarak nitelendirilebilmesi için, aşağıdakilerin tanımlanması gerekmektedir:

Çubuk Eğrisi Parametreleri
inf_strut davranış eğrisi ile birlikte modellenen yığma çubuk histeretik modelinin tanımında kullanılır. 

Kesme Eğrisi Parametreleri
inf_shear davranış eğrisi ile birlikte modellenen yığma çubuk histeretik modelinin tanımında kullanılır. 

Dolgu Panel Kalınlığı - t
Panel tuğlalarının tek başına genişliğine (örn. 12 cm) eşit olarak düşünülebilir veya sıvanın da katkısı dahil edilebilir (örn. 12+2x1,5=15 cm). 

Düzlem Dışı Yıkılma Ötelemesi 
Kat yüksekliğinin yüzdesi olarak ifade edilir ve panel elemanının devre dışı bırakılmasını (etkisizleştirme) belirler. Yani, panel  (çerçeve değil) belirli bir düzlem dışı yıkılma ötelemesine ulaştığında, düzlem dışı  mekanizma sebebiyle yıkıldığı varsayıldığından, artık yapının dayanımı ya da rijitliğine katkıda bulunmamaktadır. (Yüksek frekansa ve/veya istenmeyen ivme modlarına çok hassas olabileceğinden, ivme-tetikli devre dışı bırakılma tanıtılmamıştır. Bununla birlikte, yine de geçici bir çözüm aşağıda not 5'te önerilmiştir)

Çubuk Alanı 1 - A1
Panel kalınlığı ve eşdeğer çubuk genişliğinin (bw) çarpımı olarak tanımlanır. Eşdeğer çubuk genişliği, bir çok araştırmacı tarafından deneysel veri ve analitik sonuçlara dayanarak belirtildiği üzere, genellikle dolgu duvarın köşegeninin %10 ile %40'ı arasında değişir. Aslında, kullanıcının başvurabileceği, çeşitli yazarlar tarafından önerilen farklı derecelerde karmaşıklık gösteren bir çok ampirik ifade vardır [ör: Holmes, 1961; Stafford-Smith, 1962; Stafford-Smith and Carter, 1969; Mainstone and Weeks, 1970; Mainstone, 1971; Liauw and Kwan, 1984; Decanini and Fantin, 1986; Paulay and Priestley, 1992]. Bunlar Smyrou [2006] çalışmasında özetlenmiştir. Burada, Holmes [1961] veya Paulay & Priestley [1992] 'nin pratik önerileri bw değerini mümkün olduğunca kolaylaştırarak (hatalı olduğu anlamına gelmez) sırasıyla dm'nin 1/3 veya 1/4'ü olarak kabul etmektedir. 

Çubuk Alanı 2 - A2
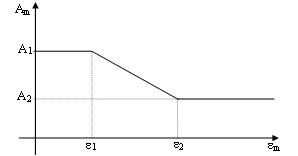
A1'in yüzdesi olarak tanımlanır. Dolgu panelin çatlaması nedeniyle, yatay ve dolayısıyla eksenel yer değiştirmeler arttıkça, çerçeve ve dolgu arasındaki temas uzunluğunun azalmasının hesaba katılmasını amaçlar. Sonuç olarak, eşdeğer çubuk alanı etkilenir. Alanın eksenel birim şekil değiştirmenin bir fonksiyonu olarak doğrusal olarak değiştiği varsayılır (bkz. alttaki figür); bu değişmenin gerçekleştiği iki birim şekil değiştirme değeri yığma çubuk histeretik model'e girdi parametreleri olarak tanımlanır.

Eşdeğer Temas Uzunluğu - hz
Panel yüksekliğinin yüzdesi olarak tanımlanır, etkin olarak dahili ve dummy düğüm noktaları arasındaki mesafe, ve çerçeve ile dolgu panel arasındaki temaz uzunluğunu bir şekilde dikkate almak için kullanılır. Stafford-Smith [1966] tarafından  değerine eşit olarak tanımlanan gerçek temas uzunluğunun (z) 1/3'ünden 1/2'sine kadar olan değerlerle makul sonuçlar elde edildiği görülmektedir. Burada,  aşağıda verilen denklemle hesaplanan birimsiz göreceli rijitlik parametresidir; Em yığma malzemenin elastik modülü, tw panelin kalınlığı, diyagonal çubuğun kirişlerle olan açısıdır, EcIc kolonların eğilme rijitliği ve hw dolgu panelin yüksekliğidir.

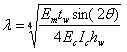
Yatay ve Düşey Kaydırmalar - xoi ve yoi
Panelin yatay ve düşey boyutlarının yüzdesi olarak tanımlanır ve çerçeve elemanlarının derinlikleri nedeniyle panelin boyutlarındaki azalmayı temsil eder. Diğer bir deyişle, bu parametreler harici ve dahili köşe düğüm noktaları arasındaki uzunluğu sağlar.

Kesmeye Atanan Rijitlik Oranı - 
Kesme yayına atanan panel rijitliği (program tarafından dahili olarka hesaplanır) oranını temsil eder (genellikle, 0,20 ve 0,60 arasında değişen bir değer kabul edilir). Diğer bir deyişle, çubuk rijitliği (KA) ve kesme rijitliği (KS) aşağıdaki gibi hesaplanır:

Özgül ağırlık - 
Panelin hacimsel ağırlığını temsil eder (bu elemana herhangi bir kesit veya malzeme atanmadığı için zati ağırlığı burada tanımlanmalıdır). Varsayılan değer 20 kN/m3'tür.

Bu elemanın iletişim kutusunda, burada açıklanan global sönümlemeye karşı, elemana-özgü sönümleme tanımlamak mümkündür. Bunu yapmak için, kullanıcıların sadece Sönümleme düğmesine basmaları ve daha sonra söz konusu elamana en iyi uyan sönümleme tipini seçmeleri gerekir (kullanıcıların mevcut olan farklı sönümleme tipleri ve daha iyi seçenek ipuçları için Sönümleme menüsüne bakmaları tavsiye edilir). Eleman seviyesinde tanımlanan sönümleme global sönümleme'den daha önceliklidir. Yani, belirli bir elemanın serbestlik dereceleri ile ilişkili "global olarak hesaplanmış" sönümleme matriks katsayıları, elemanın kütle matriksinin kütle-orantılı parametre ile çarpımından veya elemanın rijitlik matriksinin rijitlik-orantılı parametre ile çarpımından veya eleman Rayleigh sönümleme matriksi hesaplanan katsayılarla yer değiştirir.

Notlar

1. Bu model (çubuk konfigürasyonu ile), sadece en yaygın yıkılma modlarını açıklama kapasitesine sahiptir. Çünkü, bütün yığma yıkılmalarını hesaba katacak bir model kayda değer bir karmaşıklık ve belirsizlik seviyesi nedeniyle kullanışlı olmayacaktır. Kullanıcıların bu model ile ilgili daha fazla detay için Crisafulli et al. [2000] ve Smyrou et al. [2006] çalışmalarına başvurmaları şiddetle tavsiye edilir.
2. Dolgu duvarların dayanım ve rijitlikleri ilk yükler'in uygulanmasından sonra sunulur, böylece dolgu duvarlar yer çekimi yüklerini taşımaz (bu yükler, normal olarak daha önce inşa edilen çerçeve tarafından taşınır). Eğer kullanıcılar, bu yer çekimi yüklerinin dolgu duvarlar tarafından taşınmasını isterlerse, bu yükleri ilk-olmayan yükler olarak tanımlamalıdırlar. 
3. Çok detaylı modellerde, dolgu duvarların çerçeveye çoğunlukla rijit bir şekilde bağlanmamasını dikkate almak için, kullanıcılar çerçeve ve dolgu panel düğüm noktaları arasında bağlantı elemanları tanımlamak isteyebilirler.
4. Ayrıca, kullanıcılar panelin düzlem dışı yıkılmasına sebep olan belirli bir eşik sınırını aşan düzlem dışı ivme değerlerini kontrol etmek isteyebilirler (böylece, bu ivme değerlerinin ulaşılmasına karşılık gelen zaman elemanın etkisizleştirilmesi için ayarlanabilir).
5. Dolgu duvarlı çerçevelerin davranışının değerlendirilmesinde, dolgu panellerde yer alan boşluklar önemli bir belirsizlik oluşturmaktadır. Bir çok araştırmacı [örn. Benjamin and Williams, 1958; Fiorato et al., 1970; Mallick and Garg, 1971; Liauw and Lee, 1977; Utku, 1980; Dawe and Young, 1985; Thiruvengadam, 1985; Giannakas et al., 1987; Papia, 1988; Dawe and Seah, 1989; Hamburger, 1993; Bertoldi et al., 1994; CEB, 1996; Mosalam et al., 1997; Gostic and Zarnic, 1999; De Sortis et al., 1999; Asteris, 2003], boşlukların farklı konfigürasyonlarının (boyut ve yerleşim bakımından) dayanım ve rijitlik üzerine etkisini araştırmıştır. Ne yazık ki, bir şekilde anlaşılır olan çok sayıda değişken ve belirsizliğin dahil olması nedeniyle, bu konu üzerinde bir karara henüz varılamamıştır; yukarıda listelenen yayınların her biri farklı nicel sonuç ve önerilere bağlanmıştır. Bu nedenle kullanıcıların, söz konusu yapıda var olan boşlukların nasıl dikkate alınması gerektiğine karar vermesi için, kendi mühendislik muhakemesi ve deneyimleri ile literatürün bu konu hakkında kapsamlı istişaresine (yukarıda küçük bir kısmı listelenmiştir) başvurmaları gerekir. Kolaylaştırıcı bir öneri olarak, boşlukların dolgu çerçevenin davranışına etkisi, Çubuk Alanı (A1) 'nın değerini, ve dolayısıyla panelin rijitliğini, boşluk alanının panele göre orantılı olarak azaltılmasıyla dikkate alınabilir. Yani, Smyrou et al. [2006] tarafından gösterildiği üzere, eğer belirli bir dolgu panelindeki boşluklar panel alanının %15'inden %30'una kadarsa, A1 değerini (yani dayanımını) %30 ve %50 arasında değişen bir değerle azaltmakla iyi bir davranış elde edilebilir. Dolgu panelin mukavemeti söz konusu olduğunda, ve başka araştırmacılar tarafından bu konu üzerine yapılmış gözlemlerin çeşitliliği düşünüldüğünde, eğer iyi bir kanıt yoksa, kullanıcılar standart boşlukları (dolgu panelin alanının %30'undan fazla olmayan boşlukları) hesaba katmak için bu değeri değiştirmemelidirler.
6. Kullanıcılara Celarec and Dolšek [2012]’in çalışmasını okumaları tavsiye olunur. Bahsi geçen çalışmada, betonarme binalarda bulunan dolgu duvarların kesme kuvveti istemine ve kolon göçmelerine olan etkileri tarışılmaktadır ve bu etkilerin direct olarak hesaba katılamadığı basitleştirilmiş modeller kullanarak modelleme şekilleri incelenmektedir.