Ανελαστικότητα Υλικού
Τα στοιχεία κατανεμημένης ανελαστικότητας χρησιμοποιούνται ευρέως σε εφαρμογές αντισεισμικής μηχανικής, είτε για σκοπούς ερευνητικούς είτε για επαγγελματικούς σκοπούς. Ενώ τα πλεονεκτήματά τους σε σχέση με τα απλούστερα μοντέλα συγκεντρωμένης πλαστικότητας (lumped-plasticity), μαζί με μια συνοπτική περιγραφή της ιστορικής τους εξέλιξης και συζήτηση των υφιστάμενων περιορισμών, μπορούν να βρεθούν στα Filippou and Fenves [2004] ή Fragiadakis and Papadrakakis [2008], εδώ απλώς σημειώνεται ότι τα στοιχεία κατανεμημένης πλαστικότητας δεν απαιτούν (όχι απαραίτητα ευθέως) βαθμονόμηση των εμπειρικών παραμέτρων απόκρισης έναντι της απόκρισης ενός πραγματικού ή ιδανικού πλαισιακού στοιχείου υπό ιδανικές συνθήκες φόρτισης, όπως απαιτείται για τα μοντέλα φαινομενικά συγκεντρωμένης πλαστικότητας.
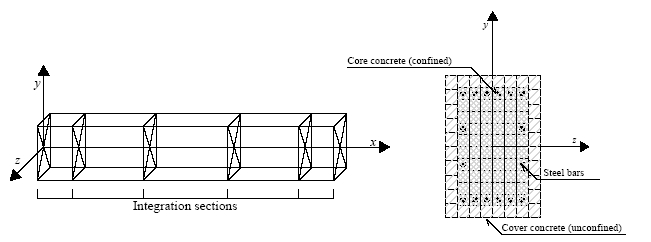
Στο SeismoStruct, χρησιμοποιείται η αποκαλούμενη μέθοδος ίνας για την προσομοίωση της συμπεριφοράς της διατομής, όπου κάθε διατομή χωρίζεται σε ίνες, καθεμία από τις οποίες συνδέεται με μία μονοαξονική σχέση τάσης-παραμόρφωσης. Τα εντατικά μεγέθη της διατομής των στοιχείων δοκού-υποστυλώματος λαμβάνονται στη συνέχεια μέσω της ολοκλήρωσης της μη γραμμικής μονοαξονικής απόκρισης τάσεως-παραμορφώσεως των ανεξάρτητων ινών (κατά προεπιλογή 100-150) στην οποία έχει υποδιαιρεθεί η διατομή (η διακριτοποίηση μιας τυπικής διατομής οπλισμένου σκυροδέματος απεικονίζεται, ως παράδειγμα, στο παρακάτω σχήμα).
Αυτά τα μοντέλα διαθέτουν σημαντικά πλεονεκτήματα, τα οποία μπορούν να συνοψιστούν ως εξής: (i) καμία απαίτηση προηγούμενης ανάλυσης ροπών-καμπυλοτήτων των μελών, (ii) δεν είναι αναγκαία η εισαγωγή παραμέτρων για την υστερητική απόκριση του στοιχείου (καθώς καθορίζεται απευθείας από τα μοντέλα των υλικών), (iii) αυτόματη προσομοίωση της αλληλεπίδρασης αξονικής φόρτισης-ροπής κάμψης (τόσο για την αντοχή όσο και για την ακαμψία) και (iv) άμεση αναπαράσταση της διαξονικής φόρτισης, και της αλληλεπίδρασης μεταξύ καμπτικής αντοχής στις δύο ορθογώνιες κατευθύνσεις.
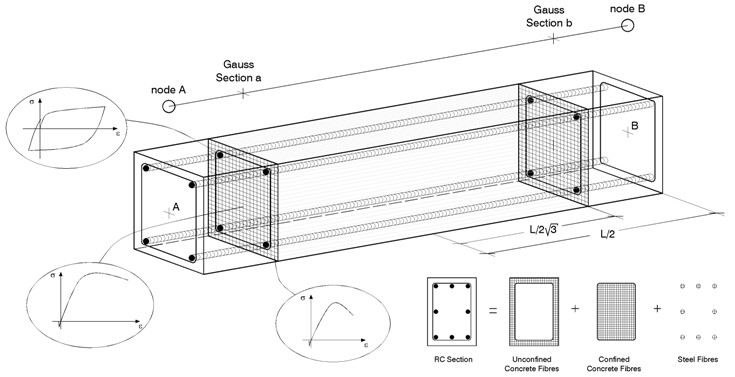
Τα πλαισιακά στοιχεία κατανεμημένης πλαστικότητας, μπορούν να υλοποιηθούν με δύο διαφορετικές διατυπώσεις πεπερασμένων στοιχείων (FE): Τα κλασικά με βάση τις μετακινήσεις (Displacement-based, DB) [e.g. Hellesland and Scordelis 1981; Mari and Scordelis 1984], και οι πιο πρόσφατες διατυπώσεις με βάση τις δυνάμεις (Force-based, FB) [e.g. Spacone et al. 1996; Neuenhofer and Filippou 1997].Στην προσέγγιση DB, επιβάλλεται το πεδίο μετακίνησης, ενώ στην FΒ, η ισορροπία του στοιχείου ικανοποιείται αυστηρώς και δεν τοποθετούνται περιορισμοί στην ανάπτυξη ανελαστικών παραμορφώσεων σε όλο το μέλος. Βλέπε π.χ. Alemdar and White [2005] and Freitas et al. [1999] για περαιτέρω επεξήγηση.
Στην περίπτωση της DB, χρησιμοποιούνται συναρτήσεις σχήματος μετακίνησης που αντιστοιχούν, για παράδειγμα, σε μια γραμμική μεταβολή της καμπυλότητας κατά μήκος του στοιχείου. Αντιθέτως, σε μια προσέγγιση FB, επιβάλλεται μία γραμμική μεταβολή ροπής, δηλαδή, η διπλή (dual) της προαναφερόμενης γραμμικής μεταβολής της καμπυλότητας. Για τη συμπεριφορά του γραμμικού ελαστικού υλικού, οι δύο προσεγγίσεις προφανώς παράγουν τα ίδια αποτελέσματα, υπό την προϋπόθεση ότι μόνο οι δυνάμεις των κόμβων δρουν επί του στοιχείου. Αντιθέτως, σε περίπτωση ανελαστικότητας των υλικών, η επιβολή ενός πεδίου μετακίνησης δεν επιτρέπει την εκτίμηση του πραγματικού παραμορφωμένου σχήματος, καθώς το πεδίο καμπυλότητας μπορεί, σε γενικές περιπτώσεις, να είναι εξαιρετικά μη γραμμικό. Σε αυτή την περίπτωση, με μια προσέγγιση DB απαιτείται μια αυξημένη διακριτικοποίηση του δομικού στοιχείου (τυπικά 4-5 στοιχεία ανά δομικό μέλος) για τον υπολογισμό των δυνάμεων/μετακινήσεων των κόμβων, προκειμένου να γίνει αποδεκτή η παραδοχή ενός πεδίου γραμμικής καμπυλότητας μέσα σε κάθε υπό στοιχείο. Επιπλέον, στην τελευταία περίπτωση οι χρήστες δεν συνιστάται να βασίζονται στις τιμές των υπολογισμένων καμπυλοτήτων των διατομών και στις επιμέρους καταστάσεις τάσης-παραμόρφωσης των ινών.
Αντ 'αυτού, μία προσέγγιση FB είναι πάντα ακριβής, αφού δεν εξαρτάται από την υποτιθέμενη συμπεριφορά της διατομής και του μέλους. Όντως δεν περιορίζει με κανέναν τρόπο το πεδίο μετακίνησης του στοιχείου. Με αυτή την έννοια αυτή η διατύπωση μπορεί να θεωρείται ως "ακριβής" πάντα, με την μοναδική προσέγγιση που εισάγεται είναι από τον διακριτό αριθμό των τμημάτων ελέγχου κατά μήκος του στοιχείου που χρησιμοποιούνται για την αριθμητική ολοκλήρωση. Απαιτούνται 4 διατομές ολοκλήρωσης Gauss-Lobatto για την αποφυγή της υπό-ολοκλήρωσης (under-integration), επιλογή που προσομοιώνει γενικά το φάσμα ελαστικότητας με αποδεκτό τρόπο. Ένα τέτοιο χαρακτηριστικό επιτρέπει την προσομοίωση κάθε δομικού στοιχείου με ένα μόνο στοιχείο FE, επιτρέποντας έτσι μια αντιστοιχία ένα προς ένα μεταξύ δομικών μελών (δοκών και υποστυλωμάτων) και στοιχείων μοντέλου. Με άλλα λόγια, θεωρητικά δεν απαιτείται κατάτμηση εντός του μέλους, ακόμα κι αν η διατομή δεν είναι σταθερή. Αυτό συμβαίνει επειδή στο πεδίο δυνάμεων είναι πάντα ακριβές, ανεξαρτήτως του επιπέδου ανελαστικότητας.
Στο SeismoStruct εφαρμόζονται και οι δύο προαναφερθείσες προσεγγίσεις στοιχείων DB και FB, με το FΒ συνήθως να συνιστάται, αφού όπως προαναφέρθηκε, γενικά δεν απαιτεί διακριτοποίηση στοιχείων, οδηγώντας έτσι σε πολύ μικρότερα μοντέλα, σε σχέση με όταν χρησιμοποιούνται στοιχεία DB, και επομένως πολύ ταχύτερες αναλύσεις, παρά τους πιο περίπλοκους υπολογισμούς ισορροπίας στοιχείου. Μια εξαίρεση από αυτόν τον κανόνα μη διακριτοποίησης, προκύπτει όταν αναμένονται ζητήματα τοπικής αστάθειας, οπότε απαιτούνται ειδικοί περιορισμοί/μέτρα, όπως συζητήθηκε στο Calabrese et al. [2010].
Επιπλέον, η χρήση ενός μεμονωμένου στοιχείου για κάθε δομικό στοιχείο δίνει στους χρήστες τη δυνατότητα της άμεσης χρήσης των αποτελεσμάτων γωνίας στροφής χορδής για την επαλήθευση των απαιτήσεων των κανονισμών (π.χ. Eurocode 8, ASCE/SEI 7-05, κλπ). Αντίθετα, όταν ένα μεμονωμένο δομικό στοιχείο πρέπει να διακριτοποιηθεί σε δύο ή περισσότερα πλαισιακά στοιχεία (απαραίτητα η περίπτωση των DB μελών), οι χρήστες πρέπει να επεξεργαστούν τα αποτελέσματα κομβικών μετακινήσεων/στροφών προκειμένου να εκτιμήσουν τη γωνία στροφής χορδής του μέλους [e.g. Mpampatsikos et al. 2008].
Τέλος, σημειώνεται ότι για λόγους μεγαλύτερης ακρίβειας, ο τετραγωνισμός Gauss χρησιμοποιείται σε εκείνες τις περιπτώσεις που δύο ή τρεις διατομές ολοκλήρωσης χρησιμοποιούνται από τον χρήστη (υπενθυμίζεται ότι το προηγούμενο είναι δυνατό μόνο για DB στοιχεία), ενώ τετραγωνισμός Lobatto χρησιμοποιείται για εκείνες τις περιπτώσεις που ορίζονται από τέσσερις έως δέκα διατομές ολοκλήρωσης. Παρόλο που οι χρήστες μπορούν να ανατρέξουν στη βιβλιογραφία ( ή σε διαδικτυακές πηγές) για περισσότερες λεπτομέρειες σχετικά με τέτοιους κανόνες, οι κατά προσέγγιση συντεταγμένες κατά μήκους του στοιχείου (μετρούμενες από το βαρύκεντρο του) δίνονται παρακάτω:
- 2 διατομές ολοκλήρωσης : [-0.577 0.577] x L/2
- 3 διατομές ολοκλήρωσης : [-1 0.0 1] x L/2
- 4 διατομές ολοκλήρωσης : [-1 -0.447 0.447 1] x L/2
- 5 διατομές ολοκλήρωσης : [-1 -0.655 0.0 0.655 1] x L/2
- 6 διατομές ολοκλήρωσης : [-1 -0.765 -0.285 0.285 0.765 1] x L/2
- 7 διατομές ολοκλήρωσης : [-1 -0.830 -0.469 0.0 0.469 0.830 1] x L/2
- 8 διατομές ολοκλήρωσης : [-1 -0.872 -0.592 -0.209 0.209 0.592 0.872 1] x L/2
- 9 διατομές ολοκλήρωσης : [-1 -0.900 -0.677 -0.363 0.0 0.363 0.677 0.900 1] x L/2
- 10 διατομές ολοκλήρωσης : [-1 -0.920 -0.739 -0.478 -0.165 0.165 0.478 0.739 0.920 1] x L/2
Σημειώσεις
- Μέσω των σχηματισμών FB λαμβάνονται άμεσα υπόψη φορτία που δρούν κατά μήκος του μέλους, ενώ αυτό δεν συμβαίνει μέσω των DB προσεγγίσεων, όπου τα κατανεμημένα φορτία πρέπει να μετασχηματιστούν σε ισοδύναμα σημειακά φορτία/ροπές στους ακραίους κόμβους του στοιχείου (και μετά πρέπει να χρησιμοποιηθεί μακρά ανάκτηση τάσης για την ανάκτηση ακριβών εντατικών δυνάμεων μέλους).
- Εφόσον ο χρήστης το επιθυμεί, έχει τη δυνατότητα να υιοθετήσει μια προσέγγιση συγκεντρωμένης πλαστικότητας που χρησιμοποιεί το ανελαστικό στοιχείο πλαστικής άρθρωσης με βάση τη μετακίνηση (infrmDBPH), σε αντίθεση με τη φιλοσοφία κατανεμημένης ανελαστικότητας εσωτερικά στα υπόλοιπα στοιχεία δοκού-υποστυλώματος στο SeismoStruct - για παράδειγμα το ανελαστικό στοιχείο πλαστικής άρθρωσης με βάση τη δύναμη (infrmFBPH) επίσης συγκεντρώνει την ανελαστικότητα στα δύο άκρα του στοιχείου, όμως σε ένα καθορισμένο μήκος του στοιχείου. Η επίδραση ίδιας μοντελοποίησης μπορεί να επιτευχθεί με χρήση του ελαστικού πλαισιακού στοιχείου δοκού-υποστυλώματος (elfrm) μαζί με μη γραμμικά στοιχεία συνδέσμου τοποθετημένα στους ακραίους κόμβους. Όμως αυτή η προσομοίωση πρέπει να χρησιμοποιείται με προσοχή, αφού η ανάλυση μπορεί να «συμβιβαστεί» όταν οι χρήστες δεν είναι έμπειροι στη βαθμονόμηση των διαθέσιμων καμπύλων απόκρισης, που χρησιμοποιούνται στον ορισμό των στοιχείων συνδέσμων, τη φύση των μη συζευγμένων ΒΕ που επίσης δεν επιτρέπουν την προσομοίωση των απαραίτητων καμπυλών/επιφανειών αλληλεπίδρασης ροπών-αξονικών φορτίων.
- Όπως προαναφέρθηκε, η προσομοίωση της κατανεμημένης ανελαστικότητας, δεν απαιτεί εμπειρία στην προσομοίωση αφού το μόνο που απαιτείται από τον χρήστη είναι η εισαγωγή των γεωμετρικών χαρακτηριστικών και των χαρακτηριστικών των υλικών των δομικών μελών (δηλ. μηχανικές παραμέτρους). Συνεπώς συνίσταται η χρήση τους και θα οδηγήσει σε μια ακριβή πρόβλεψη της μη γραμμικής απόκρισης της κατασκευής.
- Οι χρήστες καλούνται επίσης να διαβάσουν το NEHRP Seismic Design Technical Brief No. 4, στο οποίο η μη γραμμική προσομοίωση περιγράφεται αναλυτικά.