SSI Μακροστοιχείο Πασσάλων Θεμελίωσης - ssilink2

Το στοιχείο αυτό επεκτείνει την μη γραμμική προσέγγιση του μακροστοιχείου στην ανάλυση των εύκαμπτων πασσάλων με πλευρικές φορτίσεις και την αλληλεπίδραση πασσάλων με έδαφος. Βασίζεται στο έργο των Correia and Pecker [2019b]. Η πλευρική απόκριση ολόκληρου του συστήματος εδάφους-πασσάλων σε σεισμικές δράσεις συμπυκνώνεται σε ένα κεφαλόδεσμο, ο οποίος απεικονίζεται από ένα μηδενικού μήκους στοιχείο που βρίσκεται στην βάση των πασσάλων και υποβάλλεται στην κίνηση των θεμελίων, όπως φαίνεται στην παρακάτω εικόνα:

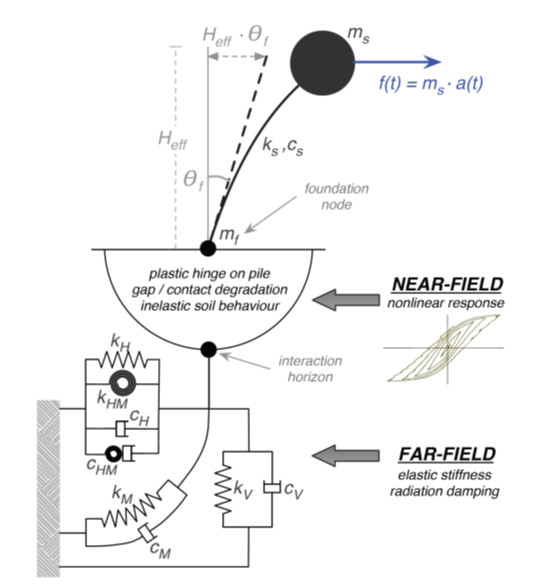
Τα μακροστοιχεία πασσάλων αντιπροσωπεύουν την πλευρική συμπεριφορά των μονών κατακόρυφων πασσάλων, που υποβάλλονται σε οριζόντιο φορτίο και σε ροπή, από τα αρχικά βήματα της φόρτισης μέχρι και την αστοχία. Οι επιδράσεις της κατακόρυφης φόρτισης δε λαμβάνονται άμεσα υπόψη σε αυτό το μοντέλο εκτός από την επίδραση της στην πλαστική ροπή της κάθετης διατομής των πασσάλων. Διαφορετικά, θεωρείται ότι η ανώτερη ζώνη του προφίλ του εδάφους, μέχρι το βάθος που θα σχηματιστεί η πλαστική άρθρωση, συμβάλλει μόνο στην πλευρική αντίσταση του φορτίου. Το κατακόρυφο φορτίο θεωρείται ότι μεταφέρεται στο έδαφος κάτω από αυτό το βάθος, όπου δεν υπάρχει επίδραση του ανοίγματος του διάκενου.

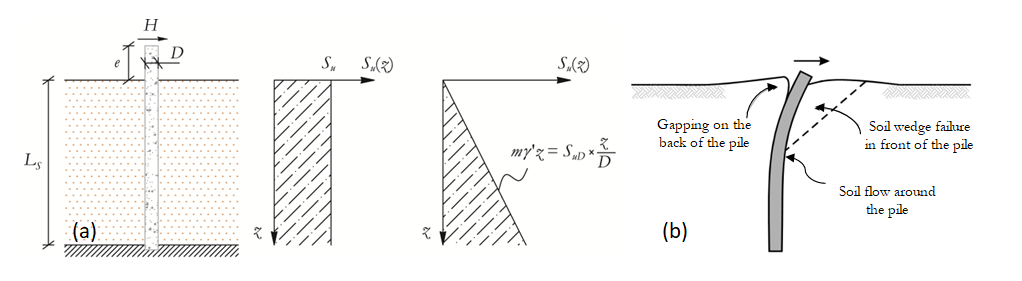
Θεωρείται μια κοιλότητα κορεσμένου εδάφους και, μετά από σεισμική κίνηση, θεωρείται ότι είναι αδιαπέραστη. Συνεπώς, το έδαφος θεωρείται ότι βρίσκεται σε αστράγγιστες συνθήκες δεδομένου ότι ο στόχος του μακροστοιχείου είναι να προσομοιώσει την απόκριση του πασσάλου υπό σεισμικές κινήσεις, ή βραχυπρόθεσμα ανακυκλιζόμενα φορτία, και το κριτήριο αστοχίας Tresca θεωρείται έγκυρο. Το σχήμα (a) αντιπροσωπεύει δύο απλουστευμένα γεωτεχνικά σενάρια, σε αστράγγιστες συνθήκες κατανομή διατμητικής αντοχής (Su) κατά μήκος του βάθους της κοιλότητας: σταθερή ή γραμμική. Το Σχήμα (b) απεικονίζει την χαρακτηριστική απόκριση εδάφους για πλευρική φόρτιση μακρύ πασσάλου, δηλαδή: μια παθητική αστοχία σε σφηνοειδές σχήμα σε μικρά βάθη και αστοχία διαρροής σε  μεγαλύτερα βάθη, με πιθανό σχηματισμό κενού πίσω από το πάσσαλο.

Το προτεινόμενο μακροστοιχείο βασίζεται σε τρία βασικά χαρακτηριστικά της συμπεριφοράς των πασσάλων που υπόκεινται σε πλευρική φόρτιση:

1. Αρχική ελαστική απόκριση,
2. Άνοιγμα και κλείσιμο κενών,
3. Συνθήκες αστοχίας φόρτισης

Το μοντέλο πλαστικότητας της οριοθετημένης επιφάνειας χρησιμοποιείται για να αντιπροσωπεύει μια συνεχή μετάβαση μεταξύ της αρχικής ελαστικής απόκρισης και της πλαστικής διαρροής, για συνθήκες φόρτισης πασσάλων μονοτονικές ή ανακυκλιζόμενες. Η συμπεριφορά απόκλισης αντιπροσωπεύεται από ένα μη γραμμικό ελαστικό μοντέλο το οποίο, ωστόσο, λαμβάνει υπόψη και επηρεάζεται από την πλαστική παραμόρφωση στο γύρω έδαφος.

Η επιφάνεια οριοθέτησης στο μακροστοιχείο αντιστοιχεί στην επιφάνεια αστοχίας για πλευρική φόρτιση των πασσάλων. Δεδομένου ότι δεν υπάρχουν στοιχεία που να δείχνουν ότι πρέπει να θεωρείται μη συσχετιστική συμπεριφορά, χρησιμοποιείται συσχετιζόμενη πλαστικότητα και η επιφάνεια οριοθέτησης λειτουργεί ταυτόχρονα ως πλαστική επιφάνεια. Σε αυτή τη σύνθεση μακροστοιχείου δεν λαμβάνεται υπόψη το αξονικό φορτίο και συνεπώς η επιφάνεια αστοχίας ορίζεται στο χώρο φόρτισης της οριζόντιας δύναμης και ροπής του πασσάλου. Επιπλέον, θεωρείται επίπεδη φόρτιση.

Μία “στρογγυλοποιημένη” προσεγγιστική επιφάνεια αστοχίας προτάθηκε από τους Correia and Pecker [2019a], η οποία βασίζεται στην λεγόμενη υπερέλλειψη. Υποθέτοντας ότι η υπερέλλειψη είναι κεντραρισμένη στο σημείο (Hc, Mc), με ένα μήκος οριζόντιου άξονα και ένα μήκος κατακόρυφου άξονα My, το οποίο επίσης υπερκαλύπτεται από την παραμόρφωση του σχήματος του, γ<0, αυτή η κατά προσέγγιση επιφάνεια αστοχίας μπορεί να εκφραστεί ως:

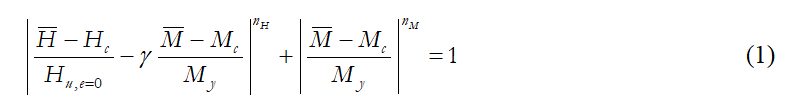
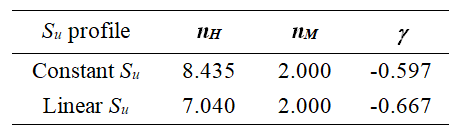
Οι θετικοί εκθέτες nH και nM καθορίζουν την καμπυλότητα των πλευρών της υπερέλλειψης. Το παρακάτω σχήμα αντιπροσωπεύει μία διαμόρφωση υπερέλλειψης, με κέντρο την αρχή των αξόνων (Hc = Mc = 0), με τις παραμέτρους της να είναι βαθμονομημένες για να ταιριάζουν σε αυτό το γραμμικό προφίλ εδάφους Su.

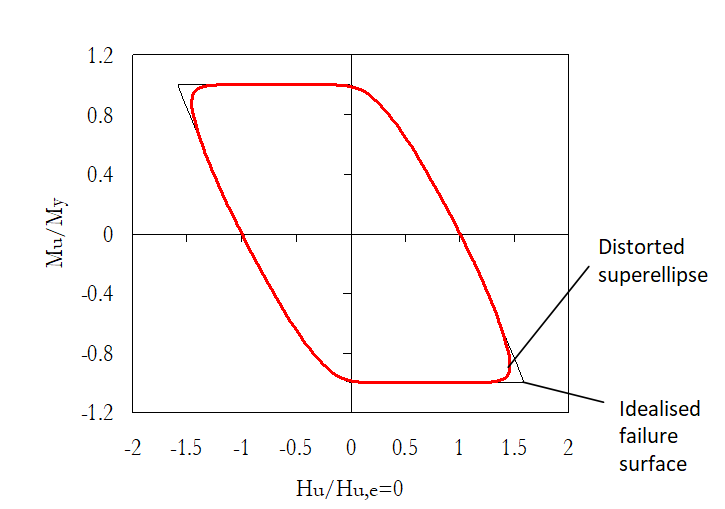
Το μοντέλο του μακροστοιχείου απαιτεί τον ορισμό 23 παραμέτρων:

• Η διάμετρος του πασσάλου (DIAM)
• Η δυσκαμψία του πασσάλου στη κάθετη, οριζόντια και περιστροφική κατεύθυνση (K_VV, K__HH, K__MM, K__HM, K__TT)
• Η ικανότητα του πασσάλου (QQ_H_MAX, QQ_M_MAX)
• Οι παράμετροι BS της υπερέλλειψης (Exp_nH,Exp_nM, GAMMA)
• Το μέγιστο βάθος κενού (ZW)
• Η καμπτική δυσκαμψία του πασσάλου (Eplp)
• Η μέγιστη παράμετρος εξέλιξης κενού (BETA)
• Η ελάχιστη παράμετρος εξέλιξης κενού (ETA)
• Το μέτρο αναφοράς της πλαστικής παραμέτρου (PL_H0)
• Ο εκθέτης για την εξέλιξη του πλαστικού μέτρου (PL_nur)
• Το χαμηλότερο όριο της τιμής για το δέλτα της αποφόρτισης/επαναφόρτισης (Delta_LIM)

Η καμπτική δυσκαμψία του πασσάλου, Eplp μπορεί να υπολογιστεί εύκολα, ενώ η ροπή διαρροής του πασσάλου, My, μπορεί να υπολογιστεί χρησιμοποιώντας οποιαδήποτε ανάλυση διατομής (και λαμβάνοντας υπόψη το στατικό κατακόρυφο φορτίο στον πάσσαλο). Διαφορετικά, οι τύποι για Hu, e=0 και zw, προέρχονται από τους Correia and Pecker [2019a].

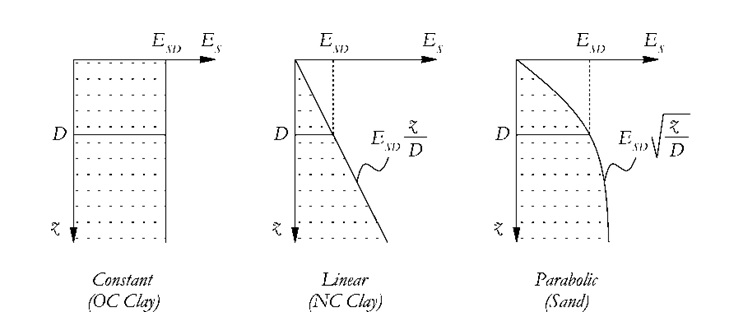
Ο Gazetas [1991] παρέχει τους τύπους για υπολογισμό της πλευρικής και αξονικής δυσκαμψίας και για τους συντελεστές απόσβεσης. Αυτά ισχύουν για εδαφικά προφίλ με σταθερή, γραμμική ή παραβολική αύξηση με το βάθος της δυσκαμψίας του εδάφους, που είναι αντιπροσωπευτικά του OC και NC, πηλού και πηλού και άμμου, αντίστοιχα. Το παρακάτω σχήμα απεικονίζει την δυσκαμψία του εδάφους σε σχέση με το βάθος σε εξιδανικευμένα εδαφικά προφίλ.

Οι εκφράσεις για στατική δυσκαμψία του πασσάλου, με μικρές τροποποιήσεις, έχουν υιοθετηθεί και από την τωρινή έκδοση του EC 8 – Part 5 [2003]. Αυτά ισχύουν για εύκαμπτους ή μακριούς πασσάλους και συνοψίζονται στον Πίνακα.

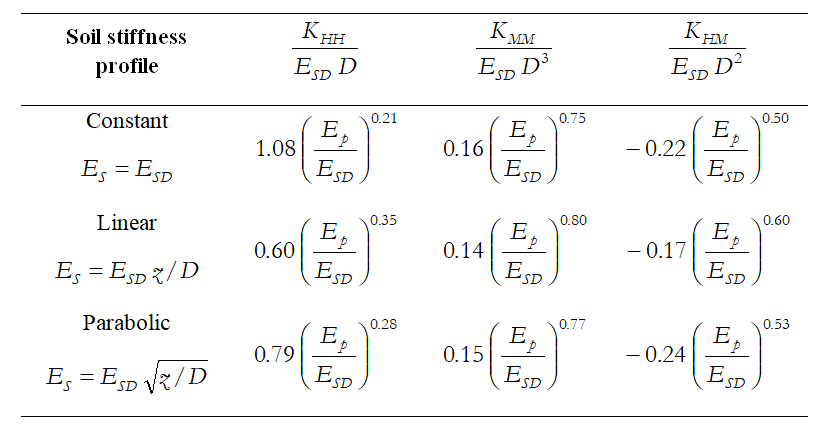
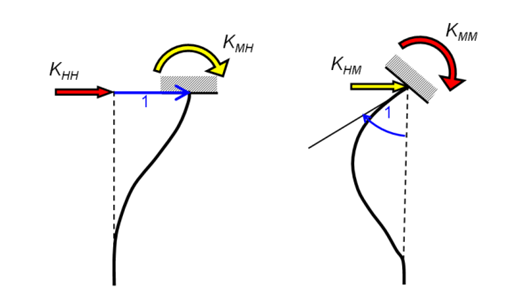
Σε αυτές τις εκφράσεις, D είναι η διάμετρος του πασσάλου, ESD είναι το μέτρο της εδαφικής παραμόρφωσης σε βάθος ίσο με τη διάμετρο του πασσάλου και Ep είναι το μέτρο Young του υλικού του πασσάλου. Οι συνιστώσες του μητρώου δυσκαμψίας του πασσάλου ακολουθούν τις συμβάσεις συμβολισμού που αναφέρονται στο παρακάτω σχήμα.

Ο Gazetas [1991] παρουσιάζει επίσης τους αντίστοιχους συντελεστές απόσβεσης του πασσάλου, οι οποίοι υπολογίζονται για κάθε συχνότητα σύμφωνα με τον παρακάτω πίνακα.

Τα δυναμικά διανύσματα της δυσκαμψίας των πασσάλων έχουν αποδειχθεί από τον Gazetas [1984] ] να είναι περίπου ίσα με ένα, για συνηθισμένο φάσμα συχνοτήτων για δομική απόκριση. Ως εκ τούτου, οι στατικές ακαμψίες του πασσάλου μπορούν να χρησιμοποιηθούν κατά προσέγγιση ως δυναμικές, για μονούς εύκαμπτους πασσάλους. Η μεταβολή των συνιστωσών του λόγου απόσβεσης με τη συχνότητα είναι γραμμική, όπως προβλέπεται από τις εκφράσεις στο παρακάτω Πίνακα. Αυτό σημαίνει ότι η συμπεριφορά της ακτινοβολίας απόσβεσης μπορεί να προσεγγιστεί με φυσικά dashpots με σταθερό συντελεστή απόσβεσης C.

Οι παράμετροι της οριοθετημένης παραμέτρου είναι σταθερές για κάθε αντοχή των εδαφικών προφίλ και παρουσιάζονται στο Πίνακα 3. Η οριακή τιμή d_Lim είναι μια παράμετρος που συσχετίζεται με την αριθμητική σύγκλιση και κυμαίνεται μεταξύ του 0,01 και 0,2 με προεπιλεγμένη τιμή 0,1.

Τέλος, οι υπόλοιπες 4 παράμετροι βαθμονόμησης, 2 από αυτές  σχετίζονται με την μονοτονική απόκριση –β και -H_o^pl  οι 2 άλλες σχετίζονται με την ανακυκλιζόμενη συμπεριφορά –η και nUR. Εναλλακτικά, 2 από τις παραμέτρους σχετίζονται με αποκλίνουσα συμπεριφορά –β και η, και οι άλλες 2 σχετίζονται με το μοντέλο πλαστικότητας -H_o^pl και nUR. Οι παράμετροι β, και nUR είναι πάντα θετικοί, ενώ η η μπορεί να είναι και ίση με μηδέν εάν δεν λαμβάνεται υπόψη το άνοιγμα του διάκενου. Οι προεπιλεγμένες τιμές και οι κλίμακες  διακύμανσης τους παρουσιάζονται στον παρακάτω πίνακα.

Σημείωση: Πρέπει να δίνεται προσοχή στην εισαγωγή σεισμών όταν εκτελείται δυναμική ανάλυση χρονοϊστορίας με SSI μακροστοιχείο. Στην πραγματικότητα, δεδομένου ότι οι δύο κόμβοι του μακροστοιχείου πρέπει να έχουν την ίδια κίνηση ενώ δεν παρουσιάζεται αδρανειακή αλληλεπίδραση, ο πιο σωστός τρόπος εκτέλεσης της ανάλυσης δεν είναι η επιβολή της χρονοϊστορίας της επιτάχυνσης του σεισμού στους κόμβους της βάσης αλλά η επιβολή των αντίστοιχων αδρανειακών δυνάμεων στις παραπάνω δομικές μάζες του κτιρίου.

Θεωρητικό υπόβαθρο στην ανάλυση SSI
Η ανάλυση SSI μπορεί να πραγματοποιηθεί μέσω της χρήσης ενός μοντέλου μη γραμμικών στερεών πεπερασμένων στοιχείων (δηλ. μπλοκ εδάφους), ή μέσω μιας απλούστερης και πιο πρακτικής προσέγγισης, η οποία είναι αυτή που υιοθετήθηκε στο SeismoStruct.

Καταρχάς κατά τη μοντελοποίηση SSI χρησιμοποιώντας τη μέθοδο της δομής, πρέπει πρώτα να αναλύσουμε την κινηματική αλληλεπίδραση του πλήρες μοντέλου του εδάφους και της δομής, με τη δομική ακαμψία αλλά χωρίς δομική μάζα. Μια τέτοια διαδικασία εισόδου σεισμικού πολλαπλασιασμού στο έδαφος είναι μοντελοποιημένη, τυπικά στις συχνότητες (αν και όχι απαραίτητα), και το τελικό αποτέλεσμα είναι η είσοδος της κίνησης των θεμελίων (FIM), δηλαδή η κίνηση του θεμελίου εάν ήταν μαζική. Αυτό το αρχικό βήμα ωστόσο συχνά αποφεύγεται υποθέτοντας ότι η κινηματική αλληλεπίδραση μπορεί να αγνοηθεί και συνεπώς να χρησιμοποιηθεί η κίνηση εδάφους ελεύθερου πεδίου ως FIM (αυτή η κίνηση ελευθέρου πεδίου θεωρείται ότι προκύπτει μόνο από την κατακόρυφη διάδοση των διατμητικών κυμάτων μέσω των οριζόντιων στρωμάτων εδάφους).

Ένα δεύτερο στάδιο της μοντελοποίησης του SSI χρησιμοποιώντας την μέθοδο της δομής θα ήταν ο υπολογισμός των αντιστάσεων της θεμελίωσης (δηλαδή ιδιότητες δυναμικής απόκρισης του θεμελίου), που αντιπροσωπεύεται συνήθως από ένα σύνολο ελατηρίων, αποσβεστήρων (και πιθανώς πλασματικές μάζες για να ληφθεί σωστή εξάρτηση των συχνοτήτων και των αντιστάσεων). Αυτό το δεύτερο βήμα μπορεί να απλοποιηθεί προσδιορίζοντας της αντιστάσεις από υπάρχουσες εκφράσεις στη βιβλιογραφία.

Το τελευταίο βήμα είναι η ανάλυση της κατασκευής, δυσκαμψία και μάζα, που στηρίζεται στις αντιστάσεις των θεμελίων και υπόκειται στο FIM. Αυτό μπορεί να γίνει στο SeimsoStruct, το οποίο διαθέτει το πρόσθετο πλεονέκτημα, μέσω της χρήσης του μακροστοιχείου SSI, να λάβει υπόψιν την μη γραμμική απόκριση του συστήματος της θεμελίωσης. Με άλλα λόγια, μία ανάλυση SSI που πραγματοποιήθηκε χρησιμοποιώντας αυτό το μακροστοιχείο αντιστοιχεί σε μια υβριδική προσέγγιση μεταξύ της ανάλυσης της αδρανειακής αλληλεπίδρασης της μεθόδου της δομής, η οποία ισχύει αυστηρά μόνο για γραμμική απόκριση και μοντελοποίηση των μη γραμμικών στερεών πεπερασμένων στοιχείων των αποτελεσμάτων του SSI.

Σύμφωνα με τα παραπάνω, ο χρήστης πρέπει να λαμβάνει υπόψη τα ακόλουθα:

1. Η μέθοδος της είναι θεωρητικά σωστή μόνο εάν η απόκριση είναι γραμμική, δηλαδή χωρίς ολίσθηση ή ανύψωση ενός θεμελίου, δημιουργία κενού λόγω πασσάλου, υποβάθμιση της δυσκαμψίας, πλαστική συμπεριφορά, και μη αναστρέψιμες μετακινήσεις. Επομένως λόγω της μη γραμμικότητας, αυτός ο τύπος ανάλυσης συνεπάγεται αναπόφευκτα κάποιο βαθμό προσεγγιστικότητας.
2. Όπως έχει ήδη αναφερθεί, η FIM είναι η κίνηση εισόδου που θα είχε η θεμελίωση αν ήταν μαζική (όπως και η υπόλοιπη κατασκευή) και αν συμπεριφερόταν γραμμικά. Πράγματι, και για παράδειγμα, εάν το μοντέλο της θεμελίωσης προσομοιώνει την αντίσταση ολίσθησης και υπάρχει δομική μάζα, η κίνηση της θεμελίωσης δεν θα υπόκειται πλέον στην FIM λόγω των αδρανειακών δυνάμεων που προέρχονται από την πάνω δομή και από μια πιθανή ολίσθηση της θεμελίωσης. Επιπλέον, ακόμη και στην περίπτωση της γραμμικής απόκρισης και στην περίπτωση μόνο του θεμέλιο με τη μάζα του (χωρίς κατασκευή από πάνω), η κίνηση του θεμελίου δεν θα είναι ακριβώς FIM λόγω των δυνάμεων αδρανείας που δημιουργούνται από την μάζα του θεμελίου.
3. Τα σεισμικά δεδομένα που εισάγονται για την SSI ανάλυση χρησιμοποιώντας την δομική προσέγγιση (όπως γίνεται στο SeismoStruct) μπορεί να είναι ένα από τα ακόλουθα:

1. • Επιταχυνσιογράφημα χρονοϊστορίας σε έναν σταθερό κόμβο βάσης του μακροστοιχείου (αυτό θα πρέπει να είναι FIM, που συχνά θεωρείται ισοδύναμο με την κίνηση ελεύθερου πεδίου, όπως έχει ήδη συζητηθεί), το οποίο στη συνέχεια θα διαδοθεί μέσω του μακροστοιχείου και θα διεγείρει τις δομικές μάζες (συμπεριλαμβανομένης και της θεμελίωσης)
   • Οι αδρανειακές δυνάμεις χρονοϊστορίας, υπολογίζονται ως το προϊόντων δομικών μαζών (συμπεριλαμβανομένης της θεμελίωσης) από το FIM, που εφαρμόζεται σε κάθε μία από της μάζες της δομής.

Αυτές οι δύο σεισμικές προσεγγίσεις εισόδου υποτίθεται ότι πρέπει να οδηγούν σε πανομοιότυπα αποτελέσματα ανάλυσης όσον αναφορά για κομβικές σχετικές μετακινήσεις (και συνεπώς παραμορφώσεις/ τάσεις υλικού και εσωτερικές δυνάμεις του στοιχείου). Η πρώτη προσέγγιση είναι ευκολότερο να εφαρμοστεί επειδή χρειάζεται να καθοριστεί μόνο η κίνηση βάσης στους σταθερούς κόμβους. Ωστόσο, μπορεί να προκαλέσει αριθμητικά προβλήματα σε ειδικές περιπτώσεις, όταν οι δυσκαμψίες του μακροστοιχείου είναι πολύ μεγάλες. Η δεύτερη προσέγγιση είναι πιο δύσκολο να εφαρμοστεί, καθώς πρέπει να εφαρμοστεί μια δυναμική δύναμη χρονοϊστορίας σε όλους τους κόμβους με συγκεντρωμένη μάζα και γίνεται δυσκίνητη όταν χρησιμοποιούνται διανεμημένες μάζες. Αλλά αυτή η μέθοδος λειτουργεί σε όλες τις περιπτώσεις.

Τοπικοί Άξονες και Προσανατολισμός Εσωτερικών Δυνάμεων