Τριγραμμική ασύμμετρη καμπύλη - trl_asm

Αυτή είναι μια καμπύλη που χρησιμοποιείται συχνά για την προσομοίωση ιδεατής τριγραμμικής ασύμμετρης συμπεριφοράς. Χρησιμοποιείται ένας κανόνας ισοτροπικής κράτυνσης. Δέκα παράμετροι πρέπει να οριστούν προκειμένου να χαρακτηριστεί πλήρως αυτή η καμπύλη απόκρισης:

Αρχική δυσκαμψία στη θετική περιοχή (K0+)
Η προεπιλεγμένη τιμή είναι 1000

Μετακίνηση πρώτου κλάδου στη θετική περιοχή (d1+)
Η προεπιλεγμένη τιμή είναι 1

Δυσκαμψία δεύτερου κλάδου στη θετική περιοχή (K1+)
Η προεπιλεγμένη τιμή είναι 50

Μετακίνηση δεύτερου κλάδου στη θετική περιοχή (d2+)
Η προεπιλεγμένη τιμή είναι 5

Δυσκαμψία τρίτου κλάδου στη θετική περιοχή (K2+)
Η προεπιλεγμένη τιμή είναι 100

Αρχική δυσκαμψία στην αρνητική περιοχή (K0-)
Η προεπιλεγμένη τιμή είναι 10000

Μετακίνηση πρώτου κλάδου στην αρνητική περιοχή(d1-)
Η προεπιλεγμένη τιμή είναι -5

Δυσκαμψία δεύτερου κλάδου στην αρνητική περιοχή (K1-)
Η προεπιλεγμένη τιμή είναι 35

Μετακίνηση δεύτερου κλάδου στην αρνητική περιοχή(d2-)
Η προεπιλεγμένη τιμή είναι -15

Δυσκαμψία τρίτου κλάδου στην αρνητική περιοχή (K2-)
Η προεπιλεγμένη τιμή είναι 100

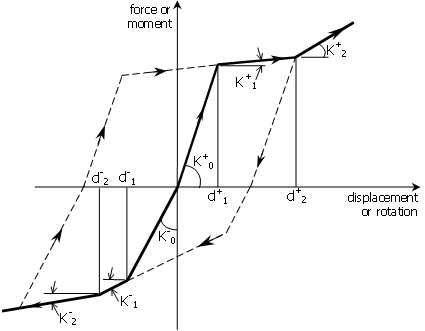
Σημειώσεις

1. Οι τιμές δυσκαμψίας  K0+, K1+, K2+ και K0-, K1-, K2-πρέπει να είναι θετικές. Ακόμη, K1 και K2 πρέπει να είναι πάντα μικρότερα από το K0 και στην θετική και στην αρνητική περιοχή μετακινήσεων.
2. Παράδειγμα. Προκειμένου να προσομοιώσετε το πρόσκρουση δύο παρακείμενων κτιρίων που χωρίζονται από ένα κόμβο-αρμό 20 mm, θα μπορούσαν να χρησιμοποιηθούν οι ακόλουθες trl_asm παράμετροι καμπύλης: K0+ = 1e12, d1+ = 0, K1+ = 0, d2+ = 1e10, K2+ = 0, K0- = 1e12, d1- = 0, K1- = 0, d2- = -20, K2- = 1e10. Όμως για αυτές τις περιπτώσεις συνίσταται η χρήση καμπύλης απόκρισης gap_hk.
3. Οι χρήστες μπορεί να ανατρέξουν στην εικόνα εδώ, για περισσότερες ενδείξεις στους κυκλικούς κανόνες που χρησιμοποιούνται σε αυτήν την καμπύλη απόκρισης. Τελικά, συνίσταται πάντα στους  χρήστες να εκτελούν απλές αναλύσεις κυκλικής φόρτισης (π.χ. χρησιμοποιώντας ένας στοιχείο μονού συνδέσμου, συνδεδεμένου στο έδαφος στη μια άκρη, και μετά επιβάλλοντας κυκλικές μετακινήσεις στον ελεύθερο κόμβο του) προκειμένου να αποκτήσετε πλήρη κατανόηση αυτής της υστερητικής σχέσης πριν τη χρήση της σε πιο περίπλοκα μοντέλα.