Ανάλυση Λυγισμού

Γενικά για να προσδιοριστεί το οριακό σημείο που ορίζει τη μετάβαση από μία σταθερή σε μία ασταθής δομή, θα πρέπει να πραγματοποιηθεί μια αυξητική ανάλυση. Η αυξητική ανάλυση λαμβάνει υπόψη τόσο τις γεωμετρικές όσο και τις μη γραμμικές ιδιότητες του υλικού. Σε ορισμένες περιπτώσεις δηλαδή λεπτών μεταλλικών κατασκευών, η σταθερότητα ορίζεται από τις γεωμετρικές μη γραμμικότητες. Επομένως αγνοώντας τη μη γραμμικότητα του υλικού και υποθέτοντας ότι η σχετική κατανομή της εσωτερικής δύναμης είναι ίση με όλα τα ποσά του εφαρμοζόμενου φορτίου μπορεί να εκτελεστεί μια ανάλυση λυγισμού αντί για μια αυξητική ανάλυση. Εκτός από αυτές τις δύο παραδοχές, τα μητρώα της γεωμετρικής ακαμψίας του στοιχείου είναι γραμμικές λειτουργίες των τελικών δυνάμεων τους. Έτσι, αυτές οι υποθέσεις επιτρέπουν να γραφεί μία καθολική εξίσωση ακαμψίας με μορφή ενός γενικευμένου ιδιομορφικού προβλήματος στο οποίο η εξίσωση της ισορροπίας στην κρίσιμη κατάσταση είναι:

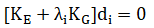
όπου K_E είναι το γραμμικό μητρώο ελαστικής δυσκαμψίας, K_G είναι το μητρώο γεωμετρικής δυσκαμψίας το οποίο αντιστοιχεί στη μεταβολή της δυσκαμψίας που προκύπτει από αλλαγές στη γεωμετρία καθώς αυξάνεται η εφαρμοζόμενη φόρτιση. Υπολογίζεται για ένα πρότυπο φόρτωσης αναφοράς P_ref  το οποίο αντιστοιχεί στη κατάσταση της βάσης με προφορτίσεις, λ_i είναι ένα διάνυσμα συντελεστών φορτίου (ιδιοτιμές) σε σχέση με το P_ref και το d_i είναι το σχήμα του τρόπου λυγισμού (ιδιοδιανύσματα), όπου i αναφέρεται στον τρόπο λειτουργίας ith λογισμικού λυγισμού. Η μικρότερη τιμή του λ_i δίνει το ελαστικό κρίσιμο φορτίο του διανύσματος λ_min P_ref. Συνήθως, είναι ευκολότερο να λυθούν αυτού του είδους προβλήματα παρά να λυθεί μία αυξητική ανάλυση.