Kazık başı makro-elemanı - ssilink2
Bu eleman modeli, yanal olarak yüklenmiş esnek kazıkların ve zemin-kazık-yapı etkileşiminin analizine yönelik doğrusal olmayan makro eleman yaklaşımını içerip, Correia ve Pecker [2019b]’in çalışmasına dayanmaktadır. Zemin-kazık sisteminin sismik etkilerde gösterdiği yatay davranış kazık başında tanımlanan sıfır uzunluklu (boyutsuz) bir elemanla temsil edilir (aşağıda gösterildiği gibi).
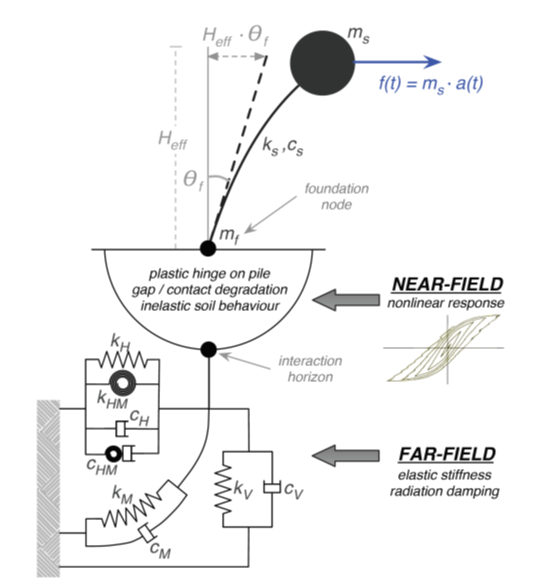
Kazık-başlı makro eleman modeli, tekil düşey kazıkların yatay yük veya moment altındaki yatay doğrultudak idavranışını başlagıç aşamalarından göçmeye kadar temsil eder. Düşey yükleme etkileri, kesidin plastik moment üzerindeki etkisi dışında, doğrudan dikkate alınmaz. Zeminin plastik mafsal oluşana kadar olan yüzeysel kısmının yalnızca yatay yük dayanımına katkıda bulunacağı varsayılır. Düşey yük ise boşluk açılma durumu yoksa bu derinliğin altında bulunan zemine aktarılır.
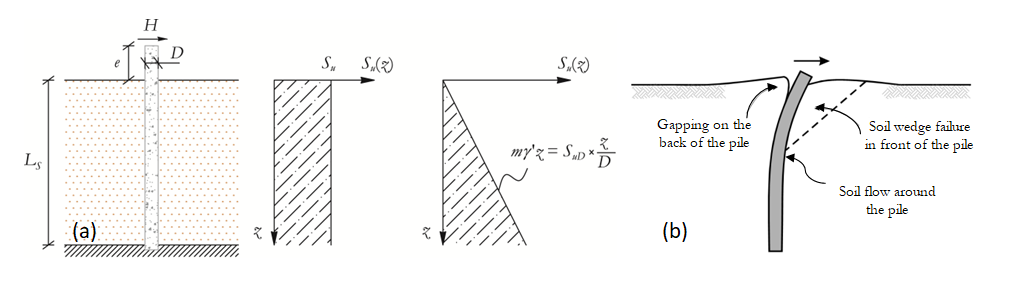
Modelde, suya doymuş bir zeminin deprem sırasında drenajsız davranacağı varsayımı baz alınır. Bu nedenle, makro eleman modeli içerisinde klasik Tresca tipi bir yüzey akma yüzeyi olarak kullanılır. Şekil 2a’da zeminde derinlik boyunca oluşan (azaltılmamış) drenajsız kesme mukavemeti (Su) dağılımının sabit ve doğrusal olmak üzere iki basitleştirilmiş dağılımı gösterilmektedir. Şekil 2b’de yanal olarak yüklenmiş uzun bir kazığa etkiyen karakteristik zemin tepkisi gösterilir. Burada, kazık arkasında boşluk oluşumu, sığ derinliklerde bulunan bir pasif kayma akması ve daha derinlerde oluşan akma (göçme) mekanizmaları gösterilmektedir.
Makro eleman, yatayyüklenenkazık-zeminetkileşimindekibulunanüç ana özelliğe dayanır:
i) İlk elastik davranış,
ii) Boşluk açılma ve kapanması
iii) Göçme yükleme koşulları.
Monotonik (tek yönlü) ve tekrarlı (tersinir) kazık-başı yükleme koşulları için başlangıçtaki elastik tepki ile plastik akma arasında sürekli bir geçişi temsil etmek için bounding surface plastisite modeli kullanılır. Boşluk davranışı, çevredeki zeminin plastik deformasyon durumunu dikkate alan ve bundan etkilenen doğrusal olmayan elastik bir modelle temsil edilir.
Makro eleman modelindeki sınırlayıcı yüzey, yanal yüklü kazık sistemi için göçme yüzeyine karşılık gelir. Bu modelde akma kuralı olarak ‘associative’ kuralı benimsenir, zira aksininin dikkate alınmasının gerektiğini gösteren herhangi bir kanıt bulunmamaktadır. Bu makro eleman formulasyonunda eksenel yük etkisi göz önüne alınmaz, dolayısıyla göçme yüzeyi yalnızca kazık başına etkiyen kesme kuvveti ve momente göre formule edilir. Ek olarak, düzlemsel bir yükleme kabul edilir.
Correia ve Pecker [2019b] tarafından önerilmiş olan ‘yuvarlatılmış’ süper eliptik bir göçme yüzeyi kullanılır. Merkezi (Hc, Mc) noktasında, yatay eksen uzunluğu ve düşey eksen uzunluğu My olan bir süperelips ele alalım ve şeklinin bozulması koşulunu (g< 0) da üzerine ekleyelim. Bu durumda formulasyon aşağıdaki gibi olacaktır.
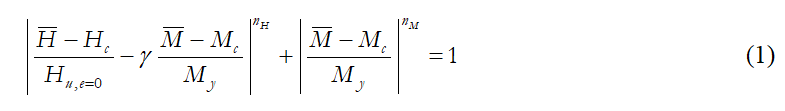
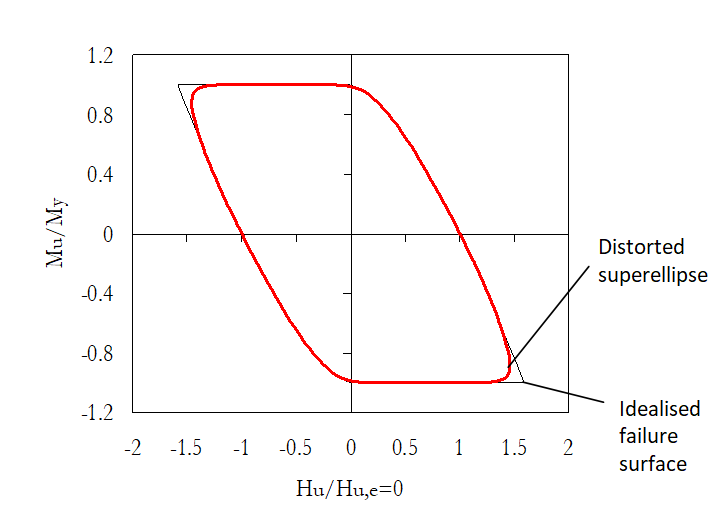
Pozitif nH ve nM üsleri, süper elipsin kenarlarının eğriliğini kontrol eder. Şekil 3, doğrusal Su profili için göçme yüzeyine uymak üzere parametreleri kalibre edilmiş olarak, başlangıçta merkezlenmiş (Hc = Mc = 0) bir bozuk-süper elips konfigürasyonunu temsil etmektedir.
Makro eleman modeli 23 parametreyle tanımlanır:
Kazık çapı (DIAM)
Dikey, yatay ve dönüş yönleri için Kazık Rijitlikleri (K_VV, K_HH,K_MM, K_HM, K_TT)
Kazık Kapasitesi (QQ_H_MAX, QQ_M_MAX)
Süper elips BS parametreleri (Exp_nH,Exp_nM, GAMMA)
Maksimum Boşluk derinliği (ZW)
Kazık Eğilme Rijitliği (Eplp)
Boşluk Gelişimi Parametresi (BETA)
Minimum Boşluk Gelişimi Parametresi (ETA)
Referans plastik modülü parametresi (PL_H0)
Plastik modül gelişimi için üs (PL_nur)
Boşaltma/yeniden yüklemede delta için alt sınır değeri (Delta_LIM)
Kazık eğilme rijitiği, Eplp, kolayca hesaplanabilirken, kazık akma momenti (My), herhangi bir kesit analiz programı kullanılarak (ve kazık üzerindeki statik dikey yük dikkate alınarak) hesaplanabilir. Öte yandan, Hu, e=0 ve zw için formüller Correia ve Pecker [2019a] çalışmasında türetilmiştir.
Gazetas [1991], kazık-kafasında tanımlaması gereken yanal ve eksenel sertlik ile sönümleme katsayılarının doğrudan hesaplanması için formüller ihtiva eder. Bunlar, sırasıyla OC kili, NC kili ve kumu temsil eden, zemin rijitliğinin derinlik ile birlikte sabit, doğrusal veya parabolik bir artışa sahip toprak profilleri için geçerlidir. Aşağıdaki şekilde bu tür idealize edilmiş zemin profillerinde derinlik ile birlikte zemin rijitliği oluşumunu temsil etmektedir.
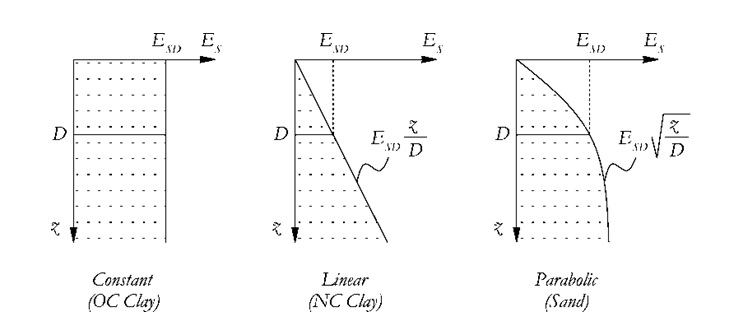
Kazık-kafasında tanımlanacak statik rijitliklere ilişkin ifadeleri, EC 8 - Bölüm 5'in [2003] mevcut versiyonunda küçük değişiklikler ile kabul edilmiştir. Bunlar esnek veya uzun kazıklar için geçerlidir ve aşağıdaki Tablo'da özetlenmiştir.
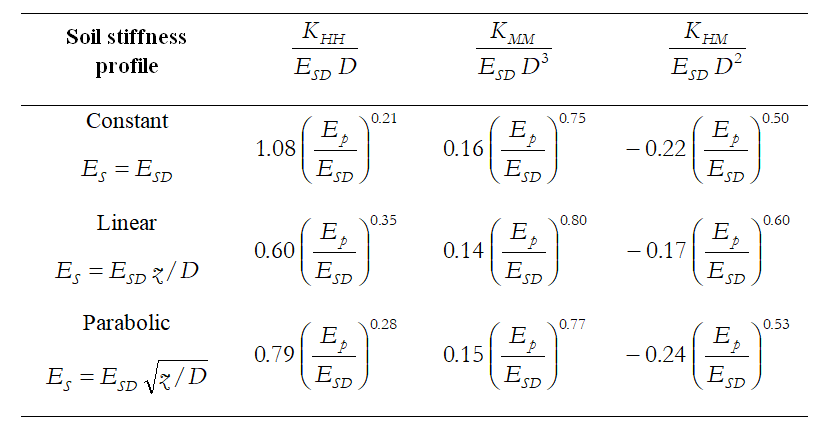
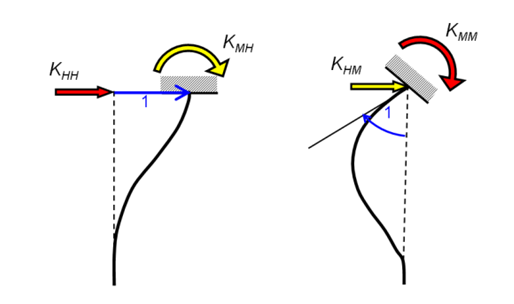
İlgili ifadelerde, D kazık çapı, ESD kazık çapına eşit bir derinlikteki zemin deformasyon modülüdür ve Ep kazık malzemesinin Young modülüdür. Kazık-kafası rijitlik matrisi bileşenleri, aşağıdaki Şekil'de ifade edilen işaret sistemine uygundur
Gazetas [1991] ayrıca, aşağıdaki Tablo'daki ifadelere göre her bir frekans f için hesaplanan karşılık gelen kazık-kafası sönümleme katsayılarını da sunmaktadır.
Kazık başı rijitliklerinin dinamik bileşenlerinin, Gazetas [1984] tarafından yapısal tepki için olağan frekans aralığı için kabaca bire eşit olduğu gösterilmiştir. Bu nedenle, kazık kafası statik rijitlikleri, tek esnek kazıklar için yaklaşık olarak dinamik olanlar olarak kullanılabilir. Sönüm oranı oranı bileşenlerinin frekansla değişimi, aşağıdaki Tablo'daki ifadeler ile tahmin edildiği gibi doğrusaldır. Bu, radyasyon sönümleme davranışının sabit sönümleme katsayısı C olan sönümleyiciler ile yaklaşık olarak tahmin edilebileceği anlamına gelir.

Sınırlayıcı yüzey (bounding surface) parametreleri, zemin mukavemeti profillerinin her biri için sabittir ve aşağıdaki Tablo'da gösterilmiştir. Sınır değeri dLim nümerik yakınsama ile ilgili bir parametredir ve varsayılan değeri 0,1’dir (tanımlanabileek değer aralığıysa 0,01 ile 0,2 arasında değişir).
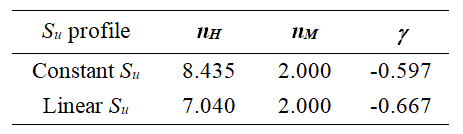
Son olarak, kalan dört kalibrasyon parametresinden, iki tanesi tek yönlü (monotonik) davranışı temsileder, bunlar: - b ve ’dir. Diğer ikisiyse tersinir (tekrarlı) yükleme davranışıyla alakalıdır (h and nUR). Diğer taraftan, yine bu parametrelerin iki tanesi (bu sefer –b ve h) boşluk açılma davranışını kontrol ederken kalan ikisi ( ve nUR) plastisite modeliyle ilgilidir. b , ve nUR her zaman pozitif degree sahiptir, h ise nihai boşluk açılmanın ele alınmadığı durumlarda sıfır olarak tanımlanabilir. Varsayılan değerleri ve varyasyon aralıkları aşağıdaki Tablo'da sunulmaktadır.

Notlar
SSI makro elementinin analizin başlangıcından itibaren doğrusal olmayan bir yanıt sunduğu göz önüne alındığında, yakınsama sorunlarından veya hatalı sonuçlardan kaçınmak için ilk yüklemeyi birkaç adımda uygulamak çok önemlidir.
SSI makro elemanı ile zaman-tanım alanlı bir dinamik analiz yapılırken, yer hareketi tanımına dikkate dilmelidir. Esasen, makro elemanın iki düğümü ataletsel etkileşim mevcut değilken aynı harekete sahip olmalıdır. Analizi gerçekleştirmenin en güvenilir yolu, temel düğümüne yer hareketini ivme tanımlı vermekten ziyade, yukarıdaki yapısal kütlelere karşılık gelen atalet kuvvetlerini tanımlamaktır.
Yerel Eksenler ve Çıktı Notasyonu

