Zemin-yapı etkileşimi eğrisi - ssi_py

Bu doğrusal olmayan dinamik zemin-yapı etkileşimi (SSI) modeli Allotey and El Naggar [2005a; 2005b] tarafından geliştirilmiş olup temel, istinat duvarı ve kazıkların değişik yük rejimleri altında analizi için kullanılabilir (seçilmiş olan terminoloji bu modelin kazıkların, genelde p-y eğrilerinin kullanıldığı, yatay yük analizinde de kullanılabileceğine dair bir delildir). Tanımlı olan ilişki; zemin göçmesinin de seçilebildiği boşluk açılmasını, değişik büyüklükteki yüklemeler altındaki tekrarlı pekleşmeyi/yumuşamayı ve ilk iskelet eğrisiyle sınırlı veya sınırsız olmak üzere davranışları modelleyebilir. Boşluk basıncı ve hacimsel değişiklikler nedeniyle meydana gelen tekrarlı yumuşama/pekleşme, 'modified rainflow counting' algoritması çerçevesinde eliptik hasar fonksiyonlarının tanımlanması yoluyla [Anthes, 1997] ve eşdeğer tekrar sayısı yaklaşımıyla [ör: Seed et al. 1975; Annaki and Lee, 1977] modellenir. Zemin göçmesiyse, ampirik olarak geliştirilmiş hiperbolik bir fonksiyon vasıtasıyla hesaba katılır.

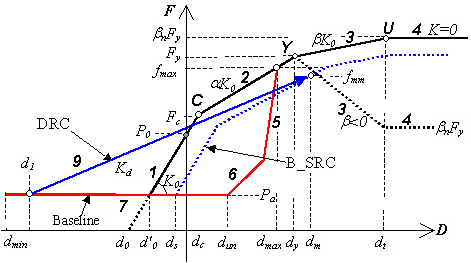
Açıkça da anlaşılabildiği üzere, histeretik model tek başına bir temel sisteminin davranışını modellemede yetersiz kalmaktadır. Herhangi bir temel sistemini modelleyebilmek için, uygun bir ssi_py eğrisine göre kalibre edilmiş bir seri yay sistemi (ör: bağlantı elemanları) bir kiriş-kolon eleman elemanıyla birlikte kullanılması şarttır. Diğer bir deyişle, davranış eğrisi doğrusal olmayan Winkler yaylarının üzerine oturan kiriş (beam-on-a-nonlinear Winkler foundation, BNWF) modeliyle tanımlanmış olur; zemini simgeleyen yayların her birine de ayrı ayrı davranış eğrisi tanımlanır. Yüzeysel temeller için yay parametreleri aynı olurken, efektif basınç derinlikle artacağından dolayı, kazık ve istinat duvarı gibi eleman/yapılar için derinliğe bağlı olarak değişir.

Ayrıca, burada da belirtildiği üzere, kullanıcıların yayılımla sönümlemeyi (radiation damping) dikkate almak istedikleri durumlarda bağlantı elemanlarına (zemin yaylarına paralel dashpt elemanları yoluyla) viskoz sönümleyiciler tanımlayabilirler. Kullanıcılar, zemin-yapı sisteminin titreşim karakteristiğine uygun sönüm katsayılarının hesaplanması için literatürde mevcut ilgili kaynaklara başvurabilirler [ör: Wolf, 1994; Allotey ve El Naggar, 2005b]. Genel olarak, zemin-yapı sisteminine ait olan doğal titreşim periyodunun sahanınkinden daha küçük olduğu durumlarda yayılımla sönümlemenin önemsiz olduğu kabul edilir.

Bu davranış eğrisinin tanımlanabilmesi için on dokuz değişken gereklidir.

İskelet eğrisinin ilk ve ikinci kısımları (K0, Fc, Fy, )
Bu modelde, zeminin düşey kuvvet-deplasman ilişkisi çok doğrulu eğri sistemiyle tanımlanır. İskelet eğrisinin ilk kısmı ilk rijitlik olan K0'a sahiptir. İkinci kısımda, Fc kuvvetinden itibaren Fy'ye olan oranıyla ifade edilir), rijitlik 'a düşer ve bu kısım zemin akma mukavemeti olan Fy'ye kadar devam eder. Bu kısımda gerekli olan parametrelerin tanım aralıkları 0 Fc < 1 ve 0.001 1 şeklindedir; varsayılan değerleri de Fc = 0.5, = 1'dir. Herhangi bir şekilde Fc 1 veya 1 tanımlanması durumunda Fc and için varsayılan değerler kullanılır.

Üçüncü ve dördüncü kısımlar - nihai eğri (ve )
Rijitlik oranını (iskelet eğrisinin üçüncü kısmının rijitliğini K0'a olan oranı) temsil eden  değişkeni ve mukavemet oranını (nihai mukavemetinin akma kuvveti olan Fy'ye oranı) temsil eden  değişkeni iskelet eğrisinin nihai davranışını belirler. Üçüncü kısmın rijitliği  (yumuşama veya pekleşme durumlarına göre) pozitif veya negatif olabilir. Pozitif olması durumunda bile ikinci kısmın rijitliğinden daha büyük olamaz ( < gerekliliği sağlanmalıdır ve program içerisinde0.9olarak kontrol edilir).

 < 0 durumundaysa iskelet eğrisinin bu kısımdaki eğiminin mutlak değeri ilk rijitlikden büyük olamaz; başka bir deyişle koşulu sağlanmalıdır.

Nihai eğrinin ikinci kısmı (iskelet eğrisinin dördüncü kısmı) her zaman sıfır eğime sahiptir. Üçüncü ve dördüncü kısımlar arasındaki geçiş noktası  (0) parametresiyle belirlenir. < 0 için <1, =0 için =1 ve >0 için >1 kullanılır. Varsayılan olarak  =0 ve =1 olup; nihai eğrinin iki kısımı da paralel bir doğruyu temsil eder (akma sonrası pekleşme veya yumuşamama olmama durumu). Herhangi bir şekilde birbirine uyumsuz  ve  parametreleri (ör: > 0 and 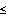1, vb) tanımlanması durumunda bu parametrelerin varsayılan değerleri kullanılır.

Nihai eğrinin negatif eğime sahip olduğu durumlarda, davranış her zaman ilk iskelet eğrisiyle sınırlı kalır; "/b" bayrağı kullanıcının tanımladığı değere bağlı kalmaksızın hep etkin konumdadır.

İlk Kuvvet (P0) ve Asgari Kuvvet (Pa)
İlk kuvvet oranı (P0) ve asgari kuvvet oranı (Pa) analiz adımlaması başlamadan önceki ilk kuvveti ve negatif deplasman altındaki asgari (aktif) kuvveti temsil eder ve Fy kuvvetiyle orantılıdır. P0 aralığı 0 P0 0,9'dur. P0 > 0 iskelet eğrisini çekme tarafına (sola) kaydırmak suretiyle sıfır deplasman durumunda mevcut olan bir ilk kuvvet tanımlar. Asgari kuvvet, Pa, modeldeki "taban" çizgisini tanımlar ve hareket hiçbir zaman bu çizginin aşağısına geçemez. Pa için 0 Pa P0 ; Pa Fy ; Pa Fc koşulları geçerlidir.

Yanal Kesme Katkı Oranı (fs)
Bu değişken, sdFc (aşağıdaki ps ve es değişkenlerine göz atınız) olarak tanımlanan yanal kesme kuvvetinin hesaba dahiliyetini belirler. Bahsi geçen etki sadece "/s" bayrağının aktif olması durumunda hesaba dahil edilir ve Pa yerine fs kullanılır (Pa=0 olursa deplasman ekseni "taban" çizgisi olur). fs değişkeninin tanım aralığı 0 fs 0,9'dur.

Boşaltma Rijitliği Değişkeni ()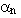
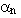, "/a" bayrağının değerine bağlı olarak, boşaltma rijitliği kaybı/pekleşmesi çarpanını sınırlayabilir ("/a" bayrağının etkisiz olması durumu) veya sabit bir boşaltma rijitliği katsayısı belirleyebilir ("/a" bayrağının etkili olması durumu). Bayrak etkiliyken,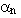> 0 olur; 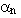> 1 koşulu boşaltma rijitliğinin iskelet eğrisindeki ilk rijitlikten büyük olması anlamına gelir (varsayılan değeri 1'dir).
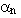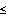
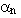
Bayrağın etkisiz olduğu durumlarda, tekrarlı boşaltma rijitliği faktörü olan ku'nun (aşağıda tanımlanan pk and ek değişkenlerine göz atınız) sınırlandırılmasında görev alır: kayıp (pk<1) için pk 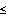1 geçerliyken pekleşme (pk>1) içinse 1 pk koşulu geçerlidir.

Model içerisinde tanımlanabilmesine karşın, birçok deneyin sonucu 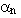değerinin "1"den çok küçük olmadığını doğrular niteliktedir. Analiz sonuçları seçilen 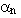değerine son derece hassastır, bu nedenle seçimi çok dikkatle yapılmalıdır, zira gerçek dışı bir 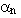çok yanlış sonuçların elde edilmesine neden olabilir.

Rijitlik/Mukavemet Kaybı/Pekleşmesi Değişkenleri (pk, ek, ps, es)
Rijitlik (pk, ek) ve mukavemet (ps, es) parametreleri tekrarlı yükleme altındaki rijitlik ve mukavemetteki kayıp ve pekleşme miktarlarını tahmin etmek için kullanılır. Bunlar, daha sonra, Allotey and El Naggar [2005a; 2005b] tarafından geliştirilen gerilmeye bağlı olmayan "eliptik" kayıp/pekleşme denklemlerinde kullanılarak rijitlik ve mukavemet kayıp/pekleşme çarpanları (ku, sd) hesaplanır. (pk, ek, ps, es) parametreleri için tanımlanabilir aralıklar pk>0, ek>0 and ps>0, es>0 şeklinde olup; kayıp pk veya ps'nin "1"den küçük olduu durumlarda meydana gelir; aksi takdirde pekleşme söz konusudur. Birçok uygulamada rijitlik ve mukavemet için kayıp veya pekleşme durumları paralel olup (rijitlik kaybı yaşanırken mukavemet artımı veya tersi beklenmez), bu durum model içerisine bir şart olarak koşulmamıştır.
ku ve sd parametreleri yarım döngü bazlı hesaplanır; dolayısıyla değerleri her bir geri yükleme veya boşaltma başlangıcında bulunur. Daha sonra, hesap edilen bu değerler hakiki iskelet eğrisinde kullanılarak mevcut geri yükleme ve genel boşaltma eğrileri elde edilir. Bahsedilen iki  çarpanın sahip olduğu kısıtlama ve sınır koşulları aşağıda belirtildiği gibidir:

  • boşaltma durumunda sadece rijitlik kaybı/pekleşmesi hesaba katılır ve tüm durumlarda sd=1 eşitliği kullanılır
  • "/a" bayrağının etkin olduğu boşaltma durumunda, tekrarlı rijitlik kaybı/pekleşmesi olmaz ve sabit bir rijitlik çarpanı kullanılır,ku = 
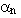
  • "/a" bayrağının etkisiz olduğu boşaltma durumunda, 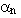azami/asgari kayıp/pekleşmeyi temsil eder, ör: pk<1 durumunda ku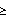 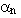olurken pk>1 durumunda ku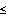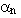olur.

Not: Varsayılan olarak bütün değerler "1"e eşittir; bu durum da kayıp veya pekleşmenin olmadığını belirtir.

S-N Eğrisi Değişkenleri (ks, f0)
S-N eğrisi tekrarlı gerilme oranının (tekrarlı gerilmenin ilk ortalama efektif gerilmeye, , oranı) yükleme tekrar sayısına göre değişmesini tanımlar; analoji olarak yorulma analizleri düşünülebilir. Yarım yükleme döngülerinin verdiği artımsal hasar kullanarak, her bir geri yükleme veya boşaltma tekrarının başında meydana gelen kümülatif kayıp/pekleşme miktarı tahmin edilir. Bu modelde, B-N eğrisi Sr = S/S1 'nin tekrar sayısına göre değişimi olarak tarif edilir; burada S ve S1 sırasıyla şimdiki ve ilk gerilme oranlarıdır. Kullanıcılar S-N eğrisini iki farklı şekilde tanımlayabilirler, "/logS" bayrağının etkili olması durumunda log-log ilişki kullanılırken, "/logS" bayrağının etkisiz olması durumundaysa yarı-logaritmik bir ilişki kullanılır. ks parametresi S-N eğrisinin eğimi olup; log-log ilişkide sıklıkla kullanılan S-N eğrisinin eğimine (ksc) eşitken yarı log ilişkide ks = ksc/S1 değerine eşittir [bkz. Allotey ve El Naggar, 2005a; 2005b].
f0 parametresi S1 değerine denk gelen zemin gerilmesidir, f0 = S1 ( ve Fy'nin birimleri aynıdır). Değişkenin tanımlı olduğu alan f0>0'dır ve varsayılan değeri f0=2Fy'dir ve ortalama tekrarlı gerilme etkisine göre ayarlanabilir, [ör: Hyodo et al., 1994].

Zeminde Boşluk Açılma Değişkenleri (p1, p2)
Boşluk açılma kuvveti değişkeni olan p1, doğrudan geri yükleme noktasının (fmm) tanımlanmasını sağlar. Doğrudan geri yükleme noktasıysa; doğrudan geri yükleme eğrisinin (DRC) birleştiği noktadır. p1 parametresi, 0 p1 1 aralığında değişebilir ve p1=0 olduğunda DRC deplasman ekseniyle paralel olarak konumlanır. "/s" bayrağının etkin olduğu ve "taban" çizgisi üzerinde seyredilen belirli bir hareketten sonra meydana gelen geri yüklemelerde boşluk açılımı sağlanır. Doğrudan geri yükleme eğrisinin (DRC), standart geri yükleme eğrisine (SRC) dönüştüğü nokta aynı zamanda DRC'nin "şimdiki taban çizgisi standart geri yükleme eğrisi" (B_SRC) ile kesiştiği noktadır. Kullanıcılar, daha fazla bilgi edinebilmek için ilgili çalışmaya bakmalıdır [Allotey ve El Naggar, 2005a; 2005b]. Varsayılan değer olarak p1=0'dır, dolayısıyla etraf basıncının etkisi tamamen ihmal edilir (böylesine bir durum sert kil-kazık arasındaki açılma davranışını modeller).
p2 parametresiyse "zemin göçmesini" dikkate alır ve B_SRC'nin başlangıç deplasmanının, ds, tayininde kullanılır. Tanım aralığı olarak 0 p2 geçerlidir, p2=0 olursa "zemin göçmesi" olmaz (diğer bir deyişle, B_SRC şimdiki boşaltma deplasman noktasından başlar). p2=0 koşulu varsayılan ayardır.

Bayrak ayarları kombinasyonu
Yukarıdaki metnin içerisinde de geçtiği üzere, bu davranış eğrisini şekillendiren beş adet bayrak vardır (/logS, /s, /b, /kbu, /a). Her bir bayrak ayrı ayrı etkinleştirilebilir (o) veya etkisizleştirilebilir (x); dolayısıyla 2^5=32 adet bayrak kombinasyonuna ulaşılabilir (bu kombinasyonlar aşağıdaki tabloda gösterilmiştir). Varsayılan bayrak kombinasyonu 31'dir; yani bütün bayraklar etkili durumdadır. Bunun da anlamı (i) log-log S-N eğrisinin kullanılması, (ii) yanal kesmenin hesaba dahil edilmesi, (iii) davranışın sınırlandırılmış olması, (iv) yük boşaltma rijitliğinin iskelet eğrisini takip etmesi ve (v) herhangi bir tekrarlı rijitlik kaybı/pekleşmesinin kullanılmadığıdır.

 
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
/logS
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
/s
x
x
x
x
x
x
x
x
o
o
o
o
o
o
o
o
x
x
x
x
x
x
x
x
o
o
o
o
o
o
o
o
/b
x
x
x
x
o
o
o
o
x
x
x
x
o
o
o
o
x
x
x
x
o
o
o
o
x
x
x
x
o
o
o
o
/kbu
x
x
o
o
x
x
o
o
x
x
o
o
x
x
o
o
x
x
o
o
x
x
o
o
x
x
o
o
x
x
o
o
/a
x
0
x
o
x
o
x
o
x
o
x
o
x
o
x
o
x
o
x
o
x
o
x
o
x
o
x
o
x
o
x
o
 

Notlar

  1. Bu gelişmiş histeretik model hala test ve gelişim altındadır. Örneğin, şu anki ssi_py eğrisi sadece dikey yük-deplasman ilişkisine göre çalışmaktadır (teğet yük-deplasman tamamen göz ardı edilmektedir). Ayrıca, (SeismoStruct'taki şu anki mevcut bağlantı elemanlarının da doğasından ötürü) serbestlik dereceleri birbirine tamemen bağlı durumda değildir. Bu unsurların, SeismoStruct'un ileriki sürümlerinde tekrar gözden geçirileceği öngörülmektedir.
  2. SeismoStruct'ın ileriki sürümlerinde, bu modelin parametrelerinin tayini/kalibrasyonu sırasında aşağı çekilen menülerin ve/veya aktif seçeneklerin bulunacağı çok daha kullanıcı dostu bir yol önerilmesi olasıdır.
  3. Geçtiğimiz yıllarda, serbestlik derecelerinin birbirleriyle tamamen bağıntılı olduğu V-H-M (Düşey (Vertical)-Yatay (Horizontal)-Dönme (Rotation)) makro modeli geliştirilmiştir [ör: Cremer at al, 2002]. Bu model, plastisite akma yüzeyi teorisini kullanarak sadece tek bir elemanla bütün temel sistemini modellemek mümkündür. Bu yeni yöntem, son derece gelecek vaad etse de şu anki gelişmişlik ve uygulanabilirlik düzeyi daha geleneksel olan BNWF modeline göre daha sınırlı olduğundan dolayı SeismoStruct'ta şu anda güçlü bir formulasyonu olan ssi_py eğrisi tanımlıdır; bu yolla gerekli statik, daha önemlisi dinamik, zemin-temel-yapı-etkileşimi yeterli bir şekilde modellenebilir.