Burkulma Analizi

Genel olarak, kararlı bir yapıdan kararsız yapıya geçişi tanıyan sınır noktasını belirlemek için artımlı bir analiz yapılmalıdır.Artımlı analiz, hem geometrik hem de malzemeyle ilintili doğrusal olmayan davranışı dikkate alır.Bazı durumlarda, (örn. narin çelik yapılar) stabilite geometrik doğrusal olmayan unsurlar tarafından kontrol edilir.Bu nedenle, doğrusal olmayan malzeme davranışını ihmal ederek, dolayısıyla uygulanan yükün her mertebedeiç kuvvetlerce eşit olarak dağılacağını kabul ederek, bir artırımlı analiz yerine burkulma analizi yapılabilir.Bu iki varsayımın yanı sıra, eleman geometrik rijitlik matrisleri eleman uç kuvvetlerinin doğrusal fonksiyonlarındandır. Yapılmış olan bu varsayımlar, global rijitlik matrisinin genelleştirilmiş özdeğer (eigenvalue) problemi olarak yazılabilmesini sağlar. Bu denklem, kritik durumda aşağıda belirtildiği gibidir.

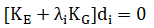
K_E: elastic rijitlik matrisi, K_G: artan yüke bağlı olarak değişen rijitliği simgeleyen geometric rijitlik matrisi. Bu değer, ön yüklerle birlikte yapının temel durumunu temsil eden referans Pref yükleme şablonuna göre hesaplanır. λ_i: Pref’e karşılık gelen yük faktörleri vektörü, di: burkulmamoduna ait şekil, i: burkulma mod sayısı. En küçük λ_i elastik kritik yük vektörüne eşit olur (λ_min). Genel olarak, bu tür bir problem çözüm stratejisi, artımsal analize nazaran daha kolaydır.