Esquema de Integración

En los análisis dinámicos no lineales debe utilizarse un esquema de integración numérica directa para resolver el sistema de ecuaciones de movimiento [por ej., Clough and Penzien, 1993; Chopra, 1995]. En SeismoBuild, dicha integración puede ser llevada a cabo mediante dos algoritmos de integración implícitos diferentes: (i) el esquema de integración de Newmark [Newmark, 1959] o (ii) el algoritmo de integración de Hilber-Hughes-Taylor [Hilber et al., 1977].

Newmark integration scheme
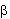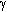El esquema de integración de Newmark requiere de la definición de dos parámetros: beta () y gama (). Es posible obtener una estabilidad incondicional, independientemente de la magnitud del incremento de tiempo utilizada, para valores de 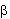>0.25(g+0.5)². Por otra parte, si se adopta 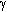= 0.5, el esquema de integración se reduce a la conocida regla trapezoidal no discipativa, en la cual no se introduce amortiguamiento numérico, condición que puede resultar ventajosa para muchas aplicaciones. 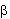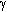Los valores por defecto son, entonces, =0.25 y =0.5.

Hilber-Hughes-Taylor integration scheme
El algoritmo de Hilber-Hughes-Taylor, por su parte, requiere la caracterización de un parámetro adicional alfa (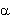) utilizado para controlar el nivel de disipación numérica. El mismo puede jugar un rol beneficioso en los análisis dinámicos, principalmente a través de la reducción de la contribución de modos altos espurios a la solución (los cuales se manifiestan típicamente en forma de picos muy altos y de breve duración), aumentando tanto la precisión de los resultados como la estabilidad numérica del análisis. De acuerdo con sus autores [Hilber et al., 1977], y como ha sido confirmado en otros estudios [por ej., Broderick et al., 1994], se obtienen soluciones óptimas, en términos de precisión de la solución, estabilidad numérica y amortiguamiento numérico, para valores de 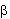=0.25(1-a)² y 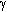=0.5-a, con -1/3£a£0. 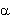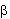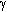En SeismoBuild, los valores por defecto son =-0.1, =0.3025 y =0.6.

Notα: Para una mayor profundización en los temas de procedimientos de solución paso-a-paso, métodos explícitos versus métodos implícitos, condiciones de estabilidad, amortiguamiento numérico, etc., se recomienda a los usuarios referirse a la literatura disponible, como los trabajos de Clough and Penzien [1993], Cook et al. [1988] y Hughes [1987], por citar algunos.