Automatic adjustment of load increment or time-step
As discussed in here, for each increment, several iterations are carried out until convergence is achieved. If convergence is not reached within the specified maximum number of iterations, the load increment (or time-step) is reduced and the analysis is restarted from the last point of equilibrium (end of previous increment or time-step). This step reduction, however, is not constant but rather adapted to the level of non-convergence verified.
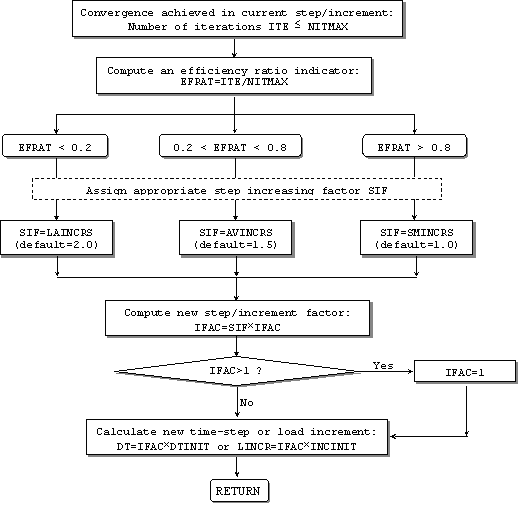
As illustrated below, at the end of a solution step or increment, a convergence ratio indicator (convrat), defined as the maximum of ratios between the achieved and the required displacement/force convergence factors (see convergence), is computed. Then, depending on how far away the analysis was from reaching convergence (convrat = 1.0), a small, average or large step reduction factor (srf) is adopted and employed in the calculation of the new step factor (ifac). The product between the latter and the initial time-step or load increment, defined by the user at the start of the analysis, yields the reduced analysis step to be used in the subsequent increment.
It is however noteworthy that, in order to prevent ill-defined analysis (which never reach convergence) to continue on running indefinitely, a user-defined lower limit for the step factor (facmin) is imposed and checked upon. If ifac results smaller than facmin then the analysis is terminated.
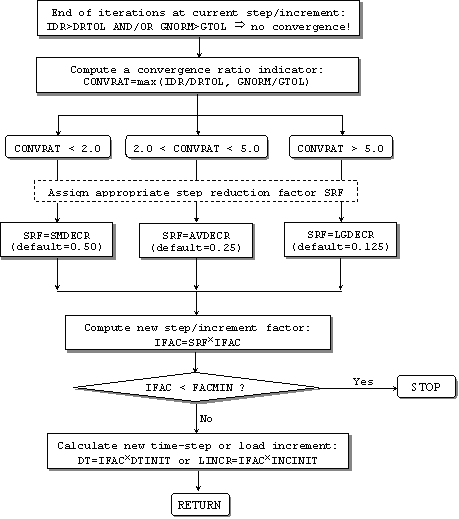
To minimise duration of analyses, it is fundamental that once convergence is reached, the load increment or time-step can be gradually increased. For this reason, an efficiency ratio indicator (efrat), defined as the ratio between the number of iterations carried out (ite) to reach convergence and the maximum number of iterations that were allowed (nitmax), is calculated. Depending on how far the analysis was from 'efficiency' (efrat > 0.8), a small, average or large step increasing factor (sif) is adopted and employed in the calculation of the new step factor (ifac). The product between the latter and the initial time-step or load increment, defined by the user at the start of the analysis, yields the augmented analysis step to be used in the subsequent increment.
It is however noteworthy that the step factor is upper-bounded by a value of 1, so as to ensure that the time step or load increment do not become larger than its initial counterpart, defined by the user at the start of the analysis.