Integration Scheme
In nonlinear dynamic analysis, a numerical direct integration scheme must be employed in order to solve the system of equations of motion [e.g. Clough and Penzien, 1993; Chopra, 1995]. In SeismoBuild, such integration can be carried out by means of two different implicit integration algorithms; the Newmark integration scheme [Newmark, 1959] and the Hilber-Hughes-Taylor integration algorithm [Hilber et al., 1977]. The latter is the default option.
Newmark integration scheme
The Newmark integration scheme requires the definition of two parameters; beta (
) and gamma (
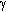). Unconditional stability, independent of time-step used, can be obtained for values of 
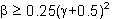. In addition, if 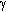= 0.5 is adopted, the integration scheme reduces to the well-known non-dissipative trapezoidal rule, whereby no amplitude numerical damping is introduced, a scenario that may prove to be advantageous on many applications. The default values are therefore = 0.25 and 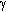= 0.5.
Hilber-Hughes-Taylor integration scheme
The Hilber-Hughes-Taylor algorithm, on the other hand, calls for the characterisation of an additional parameter alpha (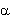
) used to control the level of numerical dissipation. The latter can play a beneficial role in dynamic analysis, mainly through the reduction of higher spurious modes' contribution to the solution (which typically manifest themselves in the form of very high short-duration peaks in the solution), thus increasing both the accuracy of the results as well numerical stability of the analysis. According to its authors [Hilber et al., 1977], and as confirmed in other studies [e.g. Broderick et al., 1994], optimal solutions, in terms of solution accuracy, analytical stability and numerical damping are obtained for values of 
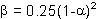and 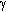= 0.5 - 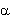, with 
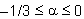. In SeismoBuild, the default values are 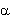= -0.1, = 0.3025 and 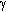= 0.6.
Note: For further discussion and clarification on issues of step-by-step solution procedures, explicit vs. implicit methods, stability conditions, numerical damping, and so on, users are strongly advised to refer to available literature, such as the work by Clough and Penzien [1993], Cook et al. [1988] and Hughes [1987], to name but a few.