Damping

In nonlinear dynamic analysis, hysteretic damping, which usually is responsible for the dissipation of the majority of energy introduced by the earthquake action, is already implicitly included within the nonlinear fibre model formulation of the inelastic frame elements  or within the nonlinear force-displacement response curve formulation used to characterise the response of link elements. There is, however, a relatively small quantity of non-hysteretic type of damping that is also mobilised during dynamic response of structures, through phenomena such friction between structural and non-structural members, friction in opened concrete cracks, energy radiation through foundation, etc, that might not have been modelled in the analysis. Traditionally, such modest energy dissipation sources have been considered through the use of Rayleigh damping [e.g. Clough and Penzien, 1993; Chopra, 1995] with equivalent viscous damping values () varying from 1% to 8%, depending on structural type, materials used, non-structural elements, period and magnitude of vibration, mode of vibration being considered, etc [e.g. Wakabayashi, 1986].

Some disagreement exists amongst the scientific/engineering community with regards to the use of equivalent viscous damping to represent energy dissipation sources that are not explicitly included in the model. Indeed, some authors [e.g. Wilson, 2001] strongly suggest for such equivalent modelling to be avoided altogether, whilst others [Priestley and Grant, 2005; Hall, 2006] advice its employment but not by means of Rayleigh damping, which is proportional to both mass and stiffness, but rather through the use of stiffness-proportional damping only; as discussed by Pegon [1996], Wilson [2001], Abbasi et al. [2004] and Hall [2006], amongst others, if a given structure is "insensitive" to rigid body motion, mass-proportional damping will generate spurious (i.e. unrealistic) energy dissipation. The stiffness-proportional damping modelling approach may then be further subdivided in initial stiffness-proportional damping and tangent stiffness-proportional damping, the latter having been shown by Priestley and Grant [2005] as the possibly soundest option for common structures.

Nonetheless, even if one would be able to include all sources of energy dissipation within a given finite elements model (and this is definitely always the best option, i.e. to explicitly model infills, dampers, SSI, etc), the introduction of even a very small quantity of equivalent viscous damping might turn out to be very beneficial in terms of the numerical stability of highly inelastic dynamic analyses, given that the viscous damping matrix will have a "stabilising" effect in the system of equations. As such, its use is generally recommended, albeit with small values. In the Damping dialog box, the user may therefore choose (i) not to use any viscous damping, (ii) to employ stiffness-proportional damping, (iii) to introduce mass-proportional damping, (iv) to utilise Rayleigh damping or (v) to utilise Automatic Rayleigh damping.

Stiffness-proportional damping
The user is asked to enter the value of the stiffness matrix multiplier (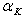) that he/she intends to use. Typically, though not exclusively, such value is computed using the following equation:

Mass-proportional damping
The user is asked to enter the value of the mass matrix multiplier (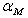) that he/she intends to use. Typically, though not exclusively, such value is computed using the following equation :

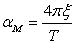
Rayleigh damping
The user is asked to enter the period (T) and damping () values of the first and last modes of interest (herein named as modes 1 and 2). The mass-proportional (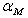) and stiffness-proportional (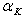) matrices multiplying coefficients are then computed by the program, using the expressions given below, which ensure that true Rayleigh damping is obtained (if arbitrarily defined coefficients would be used, this would imply that matricial rather than Rayleigh damping would be employed):

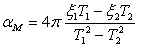__and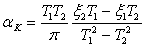

Automatic Rayleigh damping
With the automatic consideration of the values of the first and second periods along the direction of the main excitation. This last option is the program default.

Notes

1. The value of the tangent stiffness-proportional damping matrix is updated at every load increment, not at every iteration, since the latter would give rise to higher numerical instability and longer run times.
2. Should numerical difficulties arise with the use of tangent stiffness-proportional damping, the user is then advised to employ initial stiffness-proportional damping instead, using however a reduced equivalent viscous damping coefficient, so as to avoid the introduction of exaggeratedly high viscous damping effects. In other words, whilst a 2-3% viscous damping might be a reasonable assumption when analysing a reinforced structure using tangent stiffness-proportional damping, a much lower value of 0.5-1% damping should be instead employed if use is made of its initial stiffness-proportional damping counterpart.
3. Damping forces in models featuring elements of very high stiffness (e.g. bridges with stiff abutments, buildings with stiff walls, etc) may become unrealistic - overall damping in a bridge model can introduce significant damping forces, due e.g. to very high stiffness of abutments.
4. A relatively large variety of different types of matricial damping exists and is used in different FE codes. These variations may present advantages with respect to traditional Rayleigh damping; e.g. reducing the level of damping that is introduced in higher modes and so on. However, we believe that such level of refinement and versatility is not necessarily required for the majority of analysis, for which reason only the above three viscous damping modalities are featured in the program.
5. As noted above, there is significant scatter in the different proposals regarding the actual values of equivalent viscous damping to employ when running dynamic analysis of structures, and the user is advised to investigate this matter thoroughly, in order to arrive at the values that might prove to be more adequate to his/her analyses. Herein, we note simply that the value will depend on the material type (typically higher values are used in concrete, with respect to steel, for instance), structural configuration (e.g. an infilled multi-storey frame may justify higher values with respect to a SDOF bridge bent), deformation level (at low deformation levels it might be justified to employ equivalent viscous damping values that are higher than those used in analyses where buildings are pushed deep into their inelastic range, since in the latter case contribution of non-structural elements is likely to be of lower significance, for instance), modelling strategy (e.g. in fibre modelling, cracking is explicitly account for and, as such, it does not need to be somehow represented by means of equivalent viscous damping, as is done instead in plastic hinge modelling using bilinear moment-curvature relationships).