Γραμμική και Μη Γραμμική Ανάλυση

Γενικά

Στο SeismoBuild έχουν προγραμματιστεί όλες οι αναλυτικές μέθοδοι (γραμμικές και μη γραμμικές) που προτείνονται από τις προδιαγραφές, και συγκεκριμένα (i) την Γραμμική Στατική Ανάλυση (ii) την Γραμμική Δυναμική Ανάλυση (iii) την Μη Γραμμική Στατική Ανάλυση (iv) και την Μη Γραμμική Δυναμική Ανάλυση.

Γενικά, οι μη γραμμικές μέθοδοι θεωρούνται αριθμητικά πιο προηγμένες και ακριβέστερες στην αναπαράσταση της σεισμικής φόρτισης. Λαμβάνουν ρητά υπόψη τη συγκέντρωση των βλαβών στις πιο αδύναμες θέσεις του κτιρίου και την ανακατανομή των δυνάμεων κατά το σχηματισμό πλαστικών αρθρώσεων, λαμβάνοντας υπόψη τόσο την ανελαστικότητα του υλικού όσο και τις γεωμετρικές μη γραμμικότητες. Επιπλέον, η μη γραμμική δυναμική μέθοδος (αν και πιο περίπλοκη στην εφαρμογή της) θεωρείται η πιο ακριβής μέθοδος ανάλυσης, αφού καταφέρνει να αναπαραστήσει καλύτερα τη δυναμική φύση της σεισμικής φόρτισης σε σχέση με τα στατική φόρτιση. Κατά συνέπεια, οι μη γραμμικές μέθοδοι είναι αυτές που χρησιμοποιούνται κυρίως για την αξιολόγηση και την ενίσχυση υφιστάμενων κτιρίων από οπλισμένο σκυρόδεμα.

Γραμμική Στατική Ανάλυση

Με τη Γραμμική Στατική Ανάλυση (Μέθοδος Πλευρικής Δύναμης με τις συμβάσεις ονομασίας EC8) εφαρμόζεται μια τριγωνική, πλευρική, ψευδοσεισμική κατανομή που υποτίθεται ότι προσεγγίζει το φορτίο σεισμού και εφαρμόζεται σε ένα γραμμικό ελαστικό δομικό μοντέλο, προκειμένου να υπολογιστούν οι εσωτερικές δυνάμεις και τις μετατοπίσεις του συστήματος. Στη συνέχεια, αυτά τα φαινόμενα δράσης συγκρίνονται με τις ικανότητες των μελών για την επιλεγμένη στάθμη επιτελεστικότητας, πάντα ως προς τις δυνάμεις, και, εάν οι ικανότητες είναι μεγαλύτερες από τις απαιτήσεις, η δομή θεωρείται ασφαλής.

Η θεμελιώδης ιδιοπερίοδος του κτιρίου για πλευρική κίνηση προς την εξεταζόμενη διεύθυνση υπολογίζεται με ανάλυση ιδιοτιμών ή με πιο προσεγγιστικές εμπειρικές μεθόδους, από τις οποίες υπολογίζεται η τεταγμένη του φάσματος απόκρισης Sa. Η συνολική πλευρική δύναμη είναι ανάλογη με τη φασματική επιτάχυνση Sa και το βάρος του κτιρίου W

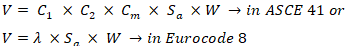
Όπου C1, C2, Cm και λ είναι εύκολα υπολογίσιμοι συντελεστές και σχετίζονται με την επίδραση των υψηλότερων ιδιομορφών και παραμέτρων, όπως οι αναμενόμενες μέγιστες ανελαστικές μετατοπίσεις, το φαινόμενο της επίδρασης του σχήματος της υστερητικής καμπύλης και την απομείωση της ακαμψίας και αντοχής. Αυτή η συνολική δύναμη κατανέμεται στη συνέχεια σε κάθε επίπεδο ορόφου, σύμφωνα με την κατανομή μάζας του κτιρίου και το ιδιομορφικό σχήμα της θεμελιώδους ιδιομορφής (στο EC8) ή μιας ανεστραμμένης τριγωνικής κατανομής (τόσο στο ASCE-41 όσο και στο EC8).

Εξαιτίας της κατά προσέγγισης φύσης της, η γραμμική στατική ανάλυση επιτρέπεται μόνο σε περιπτώσεις κανονικών, χαμηλών κατασκευών που υφίστανται περιορισμένες ζημιές και δεν υφίστανται μεγάλες ανελαστικές παραμορφώσεις.

  1. Ο λόγος απαίτησης προς ικανότητα θα πρέπει να είναι μικρή για όλα τα δομικά μέλη. Για ψαθυρούς τύπους αστοχίας, θα πρέπει να είναι κάτω της μονάδας.
  2. Δεν πρέπει να υπάρχουν ασυνέχειες και μη κανονικότητες αντοχής ή ακαμψίας εντός του επιπέδου.
  3. Δεν πρέπει να υπάρχουν ασυνέχειες και μη κανονικότητες αντοχής ή ακαμψίας εκτός του επιπέδου.
  4. Δεν πρέπει να υπάρχουν ασυνέχειες και μη κανονικότητες αντοχής ή ακαμψίας του ορόφου.
  5. Δεν πρέπει να υπάρχουν ασυνέχειες και μη κανονικότητες αντοχής στρέψης ή ακαμψίας.
  6. Η θεμελιώδης περίοδος δεν πρέπει να είναι μεγάλη.

Γραμμική Δυναμική Ανάλυση

Η Γραμμική Δυναμική Ανάλυση (Φασματική Ανάλυση, σύμφωνα με τις συμβάσεις ονομασίας EC8) είναι παρόμοια με την ΓΣΑ, τουλάχιστον όσον αφορά την προσέγγιση μοντελοποίησης. Το μοντέλο είναι και πάλι ελαστικό και δεν υπάρχει απομείωση της ακαμψίας κατά την ανάλυση. Ωστόσο, η μέθοδος είναι κάπως πιο περίπλοκη, αφού το σχήμα των πλευρικών δυνάμεων δεν είναι πλέον αυθαίρετο, αλλά υπολογίζεται ως συνδυασμός της συνεισφοράς της ιδιοπεριόδου των διαφορετικών ιδιομορφών μετακινήσεων της κατασκευής. Τα αποτελέσματα της δράσης των δομικών μελών συγκρίνονται και πάλι με την ικανότητα για την επιλεγμένη στάθμη επιτελεστικότητας ως προς τις δυνάμεις και, εάν η ικανότητα είναι μεγαλύτερη από τις απαιτήσεις, η κατασκευή θεωρείται ασφαλής. Η Γραμμική Δυναμική Ανάλυση βασίζεται στη γνωστή φασματική απόκριση (RSA) [π.χ. Rosenblueth, 1951; Chopra, 1995] και είναι η μέθοδος ανάλυσης που συνήθως χρησιμοποιείται για το σχεδιασμό νέων κατασκευών.

Η Ανάλυση Φασματικής Απόκρισης (RSA) [π.χ. Rosenblueth, 1951; Chopra, 2001; EN 1998-1, 2004] είναι μια ψευδοδυναμική μέθοδος ανάλυσης η οποία παρέχει τις μέγιστες τιμές ποσοτήτων απόκρισης, όπως οι δυνάμεις και οι μετακινήσεις, μιας κατασκευής υπό σεισμική διέγερση με μια σειρά στατικών αναλύσεων αντί για δυναμική ανάλυση χρονοϊστορίας. Σε αυτό το πλαίσιο, η χρονοϊστορία επιτάχυνσης που εισάγεται στις στηρίξεις της κατασκευής αντικαθίσταται από ισοδύναμες στατικές δυνάμεις που κατανέμονται σε όλους τους ΒΕ της κατασκευής και αντιπροσωπεύουν την συνεισφορά από κάθε φυσική ιδιομορφή. Αυτές οι ισοδύναμες δυνάμεις παράγονται ανά ιδιομορφή ως γινόμενο δύο ποσοτήτων: (1) της κατανομής ιδιομορφικής αδρανειακής δύναμης (γι΄αυτό χρειάζεται ιδιομορφική ανάλυση), και (2) της απόκρισης της ψευδο-επιτάχυνσης για κάθε ιδιομορφή της κατασκευής (που λαμβάνεται από το 5% του φάσματος απόκρισης). Για κάθε σημαντική ιδιομορφή διεξάγεται μια στατική ανάλυση, και μετά κάθε τελική μέγιστη ποσότητα απόκρισης παράγεται από τον συνδυασμό των ποσοτήτων που αντιστοιχούν σε κάθε ανάλυση.

Πρέπει να ληφθεί υπόψη ένας επαρκής αριθμός ιδιομορφών, έτσι ώστε να λαμβάνεται τουλάχιστον το 90% της συμμετέχουσας μάζας του κτιρίου σε καθεμία από τις δύο ορθογώνιες κύριες οριζόντιες κατευθύνσεις του κτιρίου, παραμελώντας έτσι μόνο τους λιγότερο σημαντικούς τρόπους δόνησης όσον αφορά τις συμμετέχοντες μάζες του κτιρίου. Το EC8 απαιτεί επίσης να λαμβάνονται υπόψη όλες οι ιδιομορφές με περισσότερο από 5% της συμμετέχουσας μάζας προς οποιαδήποτε κατεύθυνση.

Σημειώνεται ότι δεν είναι δυνατό να προσδιορίσετε την ακριβή μέγιστη τιμή κάθε ιδιομορφής, επειδή, γενικά, οι αποκρίσεις των ιδιομορφών φτάνουν σε διαφορετικές χρονικές στιγμές στη μέγιστη τιμή τους. Επομένως, εισάγονται προσεγγίσεις χρησιμοποιώντας έναν από τους κανόνες (στατιστικού) συνδυασμού των ιδιομορφών, όπως τη μέθοδο απόλυτου Αθροίσματος (ABSSUM), τη Μέθοδο της Τετραγωνικής Ρίζας του Αθροίσματος των Τετραγώνων (SRSS), και τη Μέθοδο Πλήρους Τετραγωνικού Συνδυασμού (CQC). Η CQC συνίσταται όταν οι περίοδοι έχουν κοντινές αποστάσεις, με συσχέτιση μεταξύ των ιδιομορφών. Η SRSS μπορεί να χρησιμοποιηθεί όταν οι περίοδοι διαφέρουν περισσότερο από 10%, ενώ το ABSSUM προσφέρει ένα πολύ ασφαλές, ανώτερο όριο απόκρισης.

Η ίδια διαδικασία επαναλαμβάνεται για κάθε επιθυμητή σεισμική κατεύθυνση EX, EY και EZ χρησιμοποιώντας διαφορετικά ή τα ίδια φάσματα απόκρισης. Συνήθως ζητείται να λαμβάνονται υπόψη δύο ή τρεις κατευθύνσεις σεισμικής φόρτισης ταυτόχρονα (EX, EY, EZ), μαζί με τα στατικά φορτία βαρύτητας (G+Q) της κατασκευής (η κατακόρυφη συνιστώσα EZ είναι υποχρεωτική μόνο για τα στοιχεία, όπου η κατακόρυφη δόνηση θεωρείται κρίσιμη, π.χ. μεγάλοι πρόβολοι). Οι κατευθύνσεις σεισμικής φόρτισης μπορούν να συνδυαστούν γραμμικά (E=±EX±EY±EZ) με διαφορετικούς παράγοντες fEX, fEY, fEZ για κάθε κατεύθυνση (συνήθως fEX=fEY=fEZ=1,00 ή 0,30) ή με τον κανόνα SRSS (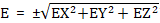). Η βαρύτητα και τα κινητά φορτία ορίζονται και προστίθενται αλγεβρικά. Επειδή τα σεισμικά φορτία λαμβάνονται υπόψη και με τα δύο πρόσημα για κάθε κατεύθυνση, τα αποτελέσματα των συνδυασμών φόρτισης RSA σε σχέση με οποιαδήποτε ποσότητα απόκρισης παρουσιάζονται ως περιβάλλουσες. Σε αντίθεση με τη Γραμμική Στατική Ανάλυση, η Γραμμική Δυναμική Ανάλυση είναι κατάλληλη για κτίρια με μεγαλύτερη θεμελιώδη περίοδο, όπου οι υψηλότερες ιδιομορφές είναι σημαντικές για το δόμημα. Εκτός από αυτό, όλες οι συστάσεις και οι περιορισμοί που περιγράφονται για την ΓΣΑ ισχύουν και για το ΓΔΑ.

  1. Ο λόγος απαίτησης προς ικανότητα DCR  θα πρέπει να είναι μικρός για όλα τα δομικά μέλη. Για τους ψαθυρούς τύπους αστοχιών, θα πρέπει να είναι κάτω από τη μονάδα.
  2. Δεν πρέπει να υπάρχουν ασυνέχειες και μη κανονικότητες αντοχής ή ακαμψίας εντός του επιπέδου.
  3. Δεν πρέπει να υπάρχει ασυνέχεια και μη κανονικότητες αντοχής ή ακαμψίας εκτός επιπέδου.
  4. Δεν πρέπει να υπάρχουν μη κανονικότητες χαμηλής αντοχής ορόφου ή ακαμψίας.
  5. Δεν πρέπει να υπάρχουν μη κανονικότητες αντοχής στρέψης ή ακαμψίας.

Μη Γραμμική Στατική Ανάλυση

Η συμβατική (μη αναπροσαρμοζόμενη) ανελαστική στατική ανάλυση (Pushover) χρησιμοποιείται για την εκτίμηση της οριζόντιας ικανότητας των κατασκευών, για τις οποίες γίνεται η υπόθεση ότι η δυναμική απόκριση τους δεν επηρεάζεται σημαντικά από τα υφιστάμενα επίπεδα παραμόρφωσης (δηλ. η κατανομή της οριζόντιας φόρτισης, που στοχεύει στην προσομοίωση της δυναμικής απόκρισης, μπορεί να θεωρηθεί περίπου σταθερή).

Τα εισαγόμενα κατακόρυφα φορτία που εφαρμόζονται στο τρισδιάστατο μοντέλο, εκτός από τα πρόσθετα φορτία, είναι ίσα με CgG+CqQ, όπου Cg και Cq είναι οι συντελεστές μόνιμων και κινητών φορτίων, αντίστοιχα, όπως ορίζονται στην καρτέλα Στατικές Δράσεις της ενότητας Προδιαγραφές Κανονισμού. Το ίδιο βάρος των στοιχείων δοκού και υποστυλώματος υπολογίζεται αυτόματα σύμφωνα με το ειδικό βάρος του υλικού και την γεωμετρία της διατομής. Τα μόνιμα, πρόσθετα μόνιμα και κινητά φορτία των πλακών εισάγονται αυτόματα ως πρόσθετη μάζα στις δοκούς. Η μη γραμμική στατική ανάλυση μπορεί να εφαρμοστεί με δύο κατακόρυφες κατανομές φορτίων:

(i) μια "ομοιόμορφη κατανομή", η οποία επιχειρεί να προσομοιώσει μια ανελαστική απόκριση που κυριαρχείται από έναν μηχανισμό μαλακού ορόφου (ανάπτυξη πλαστικών αρθρώσεων τόσο στο άνω όσο και στο κάτω άκρο όλων των υποστυλωμάτων ενός ορόφου, γενικά του ισογείου, που υπόκειται σε υψηλότερες πλευρικές δυνάμεις).

(ii) μια "ιδιομορφική κατανομή", ανάλογη με τη θεμελιώδη μεταφορική ιδιομορφή.

Τα σταδιακά φορτία μπορούν να εφαρμοστούν τόσο σε θετικές όσο και σε αρνητικές κατευθύνσεις. Επιπλέον, τα σταδιακά αυξανόμενα πλευρικά φορτία που εφαρμόζονται στην κατεύθυνση Χ και στην κατεύθυνση Υ, μπορούν να θεωρηθούν ότι δρούν ταυτόχρονα με τη χρήση και των δύο ακόλουθων συνδυασμών:

  1. ±Fx ± 0.30Fy

  2. ±0.30Fx ± Fy

Με Fx και Fy να αντιπροσωπεύουν τα σταδιακά αυξανόμενα φορτία που εφαρμόζονται στην κατεύθυνση Χ και Υ της κατασκευής, αντίστοιχα.

Τέλος, προκειμένου να ληφθούν υπόψη οι αβεβαιότητες σχετικά με τη θέση των μαζών και τη χωρική κατανομή της σεισμικής κίνησης, το υπολογιζόμενο κέντρο μάζας σε κάθε όροφο μπορεί να θεωρηθεί ότι μετατοπίζεται από την κανονική του θέση σε κάθε κατεύθυνση με τυχαία εκκεντρότητα ίση με 5% της διάστασης του ορόφου κάθετα προς την κατεύθυνση της σεισμικής δράσης.

Το εφαρμοζόμενο σταδιακά αυξανόμενο φορτίο P διατηρείται ανάλογο με το μέγεθος των ονομαστικών φορτίων (P°), που ορίζονται από το πρόγραμμα σύμφωνα με τις απαιτήσεις του αντίστοιχου Κανονισμού: P = λ(P°). Ο συντελεστής φορτίου λ αυξάνεται αυτόματα από το πρόγραμμα μέχρι να επιτευχθεί ένα όριο που καθορίζεται από τον Κανονισμό ή μέχρι να εμφανιστεί αριθμητικό πρόβλημα στις επιλύσεις. Για την αύξηση του συντελεστή φορτίου, χρησιμοποιείται στρατηγική ελέγχου μετατόπισης, η οποία αναφέρεται στην άμεση αύξηση της καθολικής μετατόπισης του κόμβου ελέγχου και στον υπολογισμό του συντελεστή φορτίου που αντιστοιχεί σε αυτήν την μετατόπιση.

Μη Γραμμική Δυναμική Ανάλυση

Η Μη Γραμμική Δυναμική Διαδικασία αποτελεί μια εξελιγμένη προσέγγιση για την εξέταση των ανελαστικών απαιτήσεων που δημιουργούνται σε μια κατασκευή από μια συγκεκριμένη σουίτα χρονοϊστοριών εδαφικής επιτάχυνσης. Όντας η αριθμητικά πιο προηγμένη μέθοδος ανάλυσης, είναι η πιο ακριβής για την αναπαράσταση της δυναμικής φύσης της σεισμικής φόρτισης. Καθώς η μη γραμμική δυναμική ανάλυση περιλαμβάνει λιγότερες παραδοχές από τη μη γραμμική στατική διαδικασία, υπόκειται και σε λιγότερους περιορισμούς από τη μη γραμμική στατική διαδικασία. Λαμβάνει αυτόματα υπόψη τις επιδράσεις των ανώτερων ιδιομορφών και μετατοπίζει τα αδρανειακά μοτίβα φόρτισης καθώς συμβαίνει πλαστικοποίηση της κατασκευής. Επιπλέον, παρέχει αξιόπιστα αποτελέσματα ακόμη και για εξαιρετικά ακανόνιστες κατασκευές ή με ακανόνιστη σεισμική δράση (π.χ. εδαφική κίνηση εγγύς πεδίου ή ταυτόχρονη φόρτιση σε 2 ή 3 κατευθύνσεις). Ως αποτέλεσμα, το NDP είναι η μόνη μέθοδος που μπορεί να χρησιμοποιηθεί για οποιαδήποτε κατασκευαστική διαμόρφωση και για κάθε τύπο φόρτισης. Στην πράξη, μπορούμε να αναλύσουμε με επαρκή ακρίβεια κάθε κατασκευαστική διαμόρφωση που υπόκειται σε οποιοδήποτε είδος σεισμικής δράσης.

Ομοίως με την ανάλυση pushover, τα εισαγόμενα κατακόρυφα φορτία που εφαρμόζονται στο τρισδιάστατο μοντέλο είναι ίσα με CgG+CqQ (ή CgG+CqQ+CsS for ASCE 41-23 και TBDY. Οι συντελεστές Cg, Cq και Cs είναι οι συντελεστές για τα μόνιμας, κινητά και φορτία χιονιού που ορίζονται στην καρτέλα Στατικές Δράσεις. Το ίδιο βάρος των στοιχείων δοκού και υποστυλώματος υπολογίζεται αυτόματα σύμφωνα με το ειδικό βάρος των υλικών και τη γεωμετρία των διατομών. Το πρόσθετο φορτίο βαρύτητας και κινητών φορτίων των πλακών εισάγονται αυτόματα ως πρόσθετη μάζα δοκών.

Η μη γραμμική δυναμική ανάλυση πραγματοποιείται εφαρμόζοντας χρονοϊστορίες επιτάχυνσης στη θεμελίωση των κτιρίων. Στο SeismoBuild οι κινήσεις εδάφους αποτελούνται από ζεύγη ορθογώνιων οριζόντιων στοιχείων εδαφικής κίνησης. Και τα δύο στοιχεία είναι τεχνητά επιταχυνσιογραφήματα συμβατά (για το επιλεγμένο επίπεδο σεισμικού κινδύνου) με το δεδομένο φάσμα στόχο ή επιταχυνσιογραφήματα ορισμένα από τον χρήστη. Στον EC8, NTC-18 και KAN.ΕΠΕ., όταν καθορίζονται 7 ή περισσότερα ζεύγη επιταχυνσιογραφημάτων, πρέπει να λαμβάνεται υπόψη η μέση απόκριση. Αντίθετα, όταν θεωρούνται λιγότερα επιταχυνσιογραφήματα, θα πρέπει να χρησιμοποιείται η δυσμενέστερη τιμή της ποσότητας απόκρισης μεταξύ των αναλύσεων στους ελέγχους επαλήθευσης. Παρομοίως, σύμφωνα με τον ASCE 41 και τον TBDY επιλέγεται μια σουίτα τουλάχιστον 11 εδαφικών κινήσεων για κάθε φάσμα στόχο και ελέγχεται η μέση απόκριση.