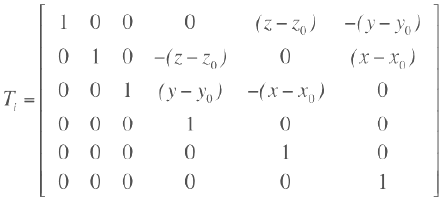Ιδιομορφικές Ποσότητες/Μάζες
Η ενότητα Ιδιομορφικές Ποσότητες/Μάζες παρέχει μια περίληψη των (i) κύριων αποτελεσμάτων της ιδιομορφικής ανάλυσης (δηλ. της περιόδου/συχνότητας των ιδιομορφών, των συντελεστών συμμετοχής των ιδιομορφών και των ενεργών ιδιομορφικών μαζών) και (ii) των επικόμβιων μαζών. Αυτά τα αποτελέσματα μπορούν εύκολα να αντιγραφούν σε ένα πρόγραμμα επεξεργασίας κειμένου, μέσω του αναδυόμενου μενού με δεξί κλικ.
Όσον αφορά τις επικόμβιες μάζες, το SeismoBuild παρέχει έναν πίνακα στον οποίο συνοψίζονται οι μάζες των κόμβων για κάθε βαθμό ελευθερίας (επίσης και οι στροφικές μάζες). Για έναν συγκεκριμένο κόμβο, η στροφική μάζα υπολογίζεται ως η στροφική μάζα που καθορίζεται από τον χρήστη για τον κόμβο αυτό, συν τη μεταφορική μάζα σε αυτόν τον κόμβο επί το τετράγωνο της απόστασης από το κέντρο βάρους του μοντέλου.
Οι συντελεστές συμμετοχής ιδιομορφών, που λαμβάνονται ως ο λόγος μεταξύ του ιδιομορφικού συντελεστή διέγερσης (modal excitation factor) (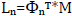 ) και της γενικευμένης μάζας (generalised mass ) (
) και της γενικευμένης μάζας (generalised mass ) (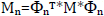 ), παρέχουν ένα μέτρο για το πόσο έντονα συμμετέχει μια δεδομένη ιδιομορφή n στη δυναμική απόκριση του δομήματος. Ωστόσο, δεδομένου ότι οι ιδιομορφές Φn μπορούν να κανονικοποιηθούν με διαφορετικούς τρόπους, το απόλυτο μέγεθος του ιδιομορφικού συντελεστή συμμετοχής δεν έχει στην πραγματικότητα κανένα νόημα και μόνο το σχετικό μέγεθός του σε σχέση με τις άλλες συμμετέχουσες ιδιομορφές είναι σημαντικό [Priestley et al., 1996].
), παρέχουν ένα μέτρο για το πόσο έντονα συμμετέχει μια δεδομένη ιδιομορφή n στη δυναμική απόκριση του δομήματος. Ωστόσο, δεδομένου ότι οι ιδιομορφές Φn μπορούν να κανονικοποιηθούν με διαφορετικούς τρόπους, το απόλυτο μέγεθος του ιδιομορφικού συντελεστή συμμετοχής δεν έχει στην πραγματικότητα κανένα νόημα και μόνο το σχετικό μέγεθός του σε σχέση με τις άλλες συμμετέχουσες ιδιομορφές είναι σημαντικό [Priestley et al., 1996].
Για τον παραπάνω λόγο, και ιδιαίτερα για την περίπτωση των κτιρίων που υποβάλλονται σε σεισμική εδαφική κίνηση, είναι σύνηθες για τους μηχανικούς/αναλυτές να χρησιμοποιούν την ενεργή ιδιομορφική μάζα (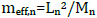 ) ως μέτρο της σχετικής σημασίας που έχει κάθε ιδιομορφή της κατασκευής στη δυναμική της απόκριση. Πράγματι, δεδομένου ότι το meff,n, μπορεί να ερμηνευθεί ως το τμήμα της συνολικής μάζας Μ της κατασκευής που διεγείρεται από μια δεδομένη ιδιομορφή n, οι ιδιομορφές με υψηλές τιμές ενεργής ιδιομορφικής μάζας, είναι πιθανόν να συμβάλλουν σημαντικά στην απόκριση.
) ως μέτρο της σχετικής σημασίας που έχει κάθε ιδιομορφή της κατασκευής στη δυναμική της απόκριση. Πράγματι, δεδομένου ότι το meff,n, μπορεί να ερμηνευθεί ως το τμήμα της συνολικής μάζας Μ της κατασκευής που διεγείρεται από μια δεδομένη ιδιομορφή n, οι ιδιομορφές με υψηλές τιμές ενεργής ιδιομορφικής μάζας, είναι πιθανόν να συμβάλλουν σημαντικά στην απόκριση.
Σημειώσεις
- Συνιστάται στους χρήστες να ανατρέχουν στη διαθέσιμη βιβλιογραφία [π.χ. Clough and Penzien, 1993; Chopra, 1995] για περισσότερες πληροφορίες σχετικά με την ανάλυση των ιδιομορφών και τις αντίστοιχες παραμέτρους.
- Οι ιδιομορφές κανονικοποιούνται έτσι ώστε Φn=1.
- Οι συντελεστές συμμετοχής ιδιομορφής για στροφή υπολογίζονται λαμβάνοντας υπόψη ένα μητρώο μετασχηματισμού που ορίζεται (x0, y0, z0 είναι οι συντεταγμένες του κέντρου μάζας), έτσι ώστε ο ιδιομορφικός συντελεστής διέγερσης να γίνει
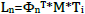 από τον οποίο προκύπτει η ενεργή ιδιομορφική μάζα (όπως για τους μεταφορικούς βαθμούς ελευθερίας).
από τον οποίο προκύπτει η ενεργή ιδιομορφική μάζα (όπως για τους μεταφορικούς βαθμούς ελευθερίας).