Μέθοδος Ολοκλήρωσης
Στη μη-γραμμική δυναμική ανάλυση, πρέπει να χρησιμοποιηθεί μια μέθοδος άμεσης αριθμητικής ολοκλήρωσης προκειμένου να λύσει το σύστημα των εξισώσεων ισορροπίας [π.χ. Clough and Penzien, 1993; Chopra, 1995].Στο SeismoBuild, αυτή η ολοκλήρωση μπορεί να εκτελεστεί μέσω δύο διαφορετικών αλγορίθμων ολοκλήρωσης τις οποίες ο χρήστης μπορεί να επιλέξει (i) την Μέθοδο Ολοκλήρωσης Newmark [Newmark, 1959] ή την (ii) Μέθοδο Ολοκλήρωσης Hilber-Hughes-Taylor [Hilber et al., 1977]. Η τελευταία είναι η προεπιλεγμένη επιλογή.
Μέθοδος ολοκλήρωσης Newmark
Η μέθοδος ολοκλήρωσης Newmark απαιτεί τον ορισμό δύο παραμέτρων: (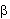 ) και (
) και (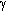 ). Για τιμές
). Για τιμές 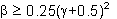 μπορεί να επιτευχθεί σταθερότητα χωρίς περιορισμούς, ανεξάρτητη από το χρησιμοποιούμενο χρονικό βήμα. Επιπλέον, εφόσον χρησιμοποιηθεί η τιμή
μπορεί να επιτευχθεί σταθερότητα χωρίς περιορισμούς, ανεξάρτητη από το χρησιμοποιούμενο χρονικό βήμα. Επιπλέον, εφόσον χρησιμοποιηθεί η τιμή 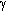 =0.5, η ολοκλήρωση ‘μειώνεται’ στο γνωστό κανόνα τραπεζοειδούς, όπου δεν χρησιμοποιείται πλάτος αριθμητικής απόσβεσης, ένα σενάριο που μπορεί να είναι ωφέλιμο σε πολλές εφαρμογές. Συνεπώς οι προεπιλεγμένες τιμές είναι
=0.5, η ολοκλήρωση ‘μειώνεται’ στο γνωστό κανόνα τραπεζοειδούς, όπου δεν χρησιμοποιείται πλάτος αριθμητικής απόσβεσης, ένα σενάριο που μπορεί να είναι ωφέλιμο σε πολλές εφαρμογές. Συνεπώς οι προεπιλεγμένες τιμές είναι 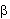 =0.25 και
=0.25 και 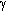 =0.5.
=0.5.
Μέθοδος ολοκλήρωσης Hilber-Hughes-Taylor
Ο αλγόριθμος Hilber-Hughes-Taylor χρειάζεται τον ορισμό μιας πρόσθετης παραμέτρου (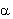 ) που χρησιμοποιείται για να ελέγξει το επίπεδο της αριθμητικής διασποράς. Το τελευταίο μπορεί να έχει ένα ευεργετικό ρόλο στη δυναμική ανάλυση, κυρίως μέσω της ‘μείωσης’ των ανώτερων χωρικών ιδιομορφών στη συνεισφορά στη λύση (οι οποίες τυπικά φανερώνονται με τη μορφή πολύ υψηλών μικρής διάρκειας κορυφών στη λύση), γι΄αυτό αυξάνει τόσο την ακρίβεια των αποτελεσμάτων όσο και την αριθμητική σταθερότητα της ανάλυσης. Σύμφωνα με τους συγγραφείς της [Hilber et al., 1977], και όπως επιβεβαιώθηκε και από άλλες μελέτες [π.χ. Broderick et al., 1994], οι βέλτιστες λύσεις σε όρους ακρίβειας λύσης, αναλυτική σταθερότητα και αριθμητική απόσβεση εκτιμώνται για τιμές
) που χρησιμοποιείται για να ελέγξει το επίπεδο της αριθμητικής διασποράς. Το τελευταίο μπορεί να έχει ένα ευεργετικό ρόλο στη δυναμική ανάλυση, κυρίως μέσω της ‘μείωσης’ των ανώτερων χωρικών ιδιομορφών στη συνεισφορά στη λύση (οι οποίες τυπικά φανερώνονται με τη μορφή πολύ υψηλών μικρής διάρκειας κορυφών στη λύση), γι΄αυτό αυξάνει τόσο την ακρίβεια των αποτελεσμάτων όσο και την αριθμητική σταθερότητα της ανάλυσης. Σύμφωνα με τους συγγραφείς της [Hilber et al., 1977], και όπως επιβεβαιώθηκε και από άλλες μελέτες [π.χ. Broderick et al., 1994], οι βέλτιστες λύσεις σε όρους ακρίβειας λύσης, αναλυτική σταθερότητα και αριθμητική απόσβεση εκτιμώνται για τιμές 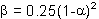 και
και 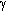 = 0.5 -
= 0.5 - 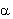 , με
, με 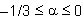 . Στο SeismoBuild, οι προεπιλεγμένες τιμές είναι
. Στο SeismoBuild, οι προεπιλεγμένες τιμές είναι 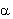 =-0.1,
=-0.1, 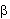 =0.3025 and
=0.3025 and 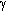 =0.6.
=0.6.
Σημείωση: Για περισσότερη συζήτηση και διασαφήνιση σε θέματα διαδικασιών λύσης βήμα προς βήμα, σαφών έναντι ‘αφηρημένων’ μεθόδων, συνθηκών σταθερότητας, αριθμητικής απόσβεσης κλπ., συνίσταται στους χρήστες να ανατρέξουν στη διαθέσιμη βιβλιογραφία, όπως για παράδειγμα τα έργα των Clough and Penzien [1993], Cook et al. [1988] και Hughes [1987].